高速电主轴滚珠轴承-转子系统 动态性能分析
2016-8-12 来源: 哈尔滨工业大学 作者: 张阿祺
转轴和支承轴承是电主轴系统的核心元件,轴承的支承性能和转轴的设计参数对系统的动态性能影响很大,电主轴转速高、功率大,是高速切削技术和高速数控机床的主体和核心部件之一,很有必要对轴承的结构参数和电主轴的设计参数进行了解。单纯研究主轴转子或单纯研究轴承都不具有很大的实际意义,需要结合轴承和电主轴转子为一体,综合研究系统的动态性能,因此,对电主轴及其支承轴承的关键参数需要具体分析。角接触球轴承的宏观受力分析是基础,但是本文还需要对轴承微观受力分析即分析轴承的内部受力状态,了解轴承中每一个球滚动体的受力载荷,进而再了解轴承在外力作用下的载荷是如何分配的。在静载荷作用下的轴承,或者是转速很低的轴承,所受到的惯性力、摩擦力和力矩等不会对球滚动体间的载荷分配产生明显的影响,因而忽略部分微小影响因素来研究静载荷作用下的球轴承。
2.1、主轴及其轴承的几何结构
如图 2-1,完整的电主轴系统主要包括:数控系统、润滑系统、过滤调压系统、油气混合系统、冷却系统、驱动系统和电主轴,本文主要研究电主轴的动态性能。
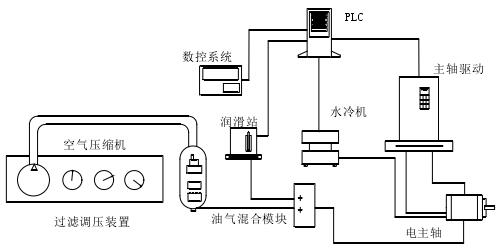
图 2-1 完整的电主轴系统
高速电主轴的轴承布局形式[43]影响着电主轴系统的刚度和动态特性,所以选择也要有的放矢,目前主要有两种结构形式,这是根据主轴的支承轴承和内置电机相对位置的不同来划分的:
(1)电主轴的内置电机安装在主轴转子的后轴承之后,也就是在两个支承轴承的外部。这种结构布局使得电主轴的轴向尺寸相对较大,对空间要求比较高,但有利于减少主轴前端的径向尺寸、散热快[44],一般应用在小高速数控机床上[45];
(2)内置电机安装在主轴转子的两个轴承之间[46],如图 2-2 所示。这种结构具有很多优点,现在的很多高速电主轴和高速数控机床都采用这种布局形式[47]。
本文主要研究角接触球轴承支承的电主轴,角接触球轴承不仅具有高制造精度、高运转稳定性、高极限转速而且还拥有很强的承载能力,是能够高速化的滚动轴承中的最佳选择,在加工中心和各类机床得到广泛应用。
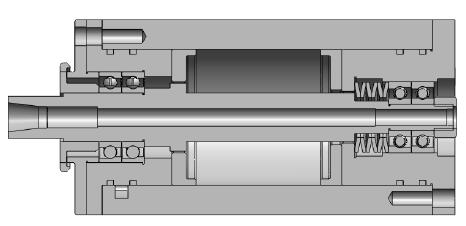
图 2-2 高速电主轴模型
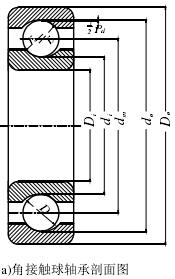
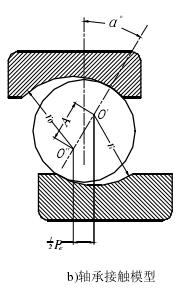
图2-3角接触球轴承7218的几何结构及参数
如图2-4为电主轴的剖面图,它包括前支承轴、后支承轴承、定子、转子、转承、轴承预紧弹簧、前盖、后盖客体等组成。
表 2-1 角接触球轴承 7218 的结构参数
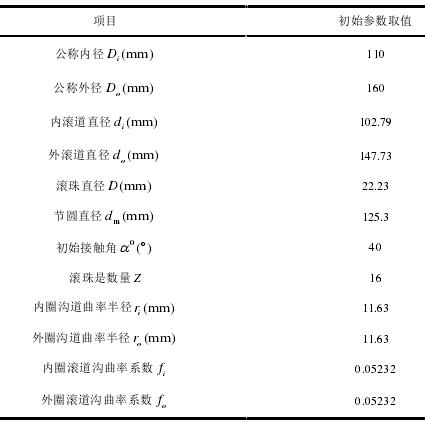
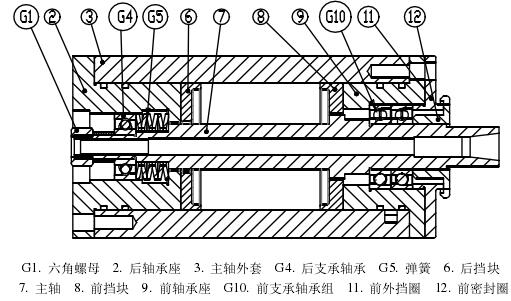
图 2-4 电主轴剖面图
考虑到本文所设计的高速电主轴的前端轴向尺寸不受限制,所以电主轴的结构布局形式采用采用第二种结构布局方式,图 2-2 和图 2-4 为此布局方式的电主轴几何结构模型和剖面图。
本文前半部分通过使用角接触球轴承 7218 进行理论分析,得出结果与相关文献[48,49]。相比较验证程序的正确性。7218 相关几何结构和参数见图 2-3 和表 2-1。
2.2、球轴承支承的电主轴设计简介
滚动轴承支承的电主轴转速高、功率大,是高速切削技术和高速数控机床的主体元件,相比传统的机床主轴,电主轴具有很多优点:
(1)传统电主轴由于齿轮和带轮等中间传动装置在生产制造时存在一定的误差,同时在安装轴承,电主轴等部件时存在安装误差,使得在电主轴高速运转时会产生一定的影响,减小了主轴转子系统的动刚度,增加了轴承和主轴转子系统的振动响应。使得机床的零件加工质量变差,加工精度降低。电主轴系统则没有中间环节,零传动的电主轴提高了零件的加工精度;
(2)零传动这一突破性的优势,使得机床在很大程度上可以实现高速加工,提高生产率和加工精度。电主轴的结构性能设计主要需要确定电主轴的 D,d,a,L 等主要结构参数。
2.2.1 电主轴平均直径D
依照国内外的电主轴生产厂家、电主轴研制机构、电主轴轴承研究所等相关部门的技术规范和参考资料,依据所选用的电机、轴承和相关的冷却套等尺寸参数,再跟据《机械工程手册》、《材料力学》、《机械工程材料》等相关资料,按以下经验公式计算:

式中P ——提供能源的传输的功率(W);
T ——转轴传递的额定转矩( N m ),9550PTn ;
——转轴的材料的许用切应力(MPa);
n ——轴的转速(r/min);
y——主轴的内直径与外直径之比, y d/ D 。
2.2.2 电主轴前端悬置量 a 的初步选取
电主轴的前悬置量 a 对主轴的综合总刚度矩阵、主轴的总体质量矩阵的影响很大,如果主轴的结构布局和主轴的空间占地大小允许的话,减小主轴轴端伸长量有点于主轴的刚度的提升,应尽可能减小主轴的轴端伸长量,以提高主轴的刚度,进而提高电主轴的性能。
2.2.3 主轴支承最佳跨距 L 设 l0为主轴支承轴承的最佳支承跨距,该跨距值符合主轴前端最小静挠度条件,是主轴在刚度、结构性能和主轴轴向尺寸大小的最佳取舍。
在外载荷 R 作用下电主轴的轴端位移变量为:
式中zy ——假设弹性轴承支承时,刚性主轴轴端位移(mm);
sy ——假设刚性轴承支承吋,弹性体主轴轴端位移(mm)。
根据材料力学梁的挠度公式:
式中E——主轴材料的弹性模量(Mpa);
I——主轴截面的平均惯量距( mm4),当主轴的内孔直径为 d,平均直径为 D 时,公式1
由几何关系可得:
假设前轴承和后支承的支反力分别为 F1、F2,其对应刚度为 K1、K2,则对应的变形可表示为:

由力平衡条件可得:

由式(2-2)、(2-3)、(2-4)可得:
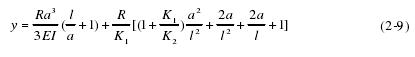
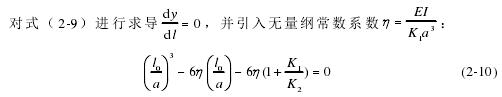

2.3、球轴承宏观几何关系
2.3.1 静载荷作用下的支承轴承
根据滚动体和滚道接触的载荷-位移关系【47】,可知径向载荷作用下的角接触球轴承:


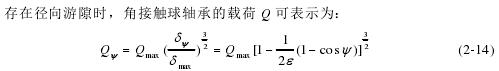

式中δr ——径向位移(mm);
dP ——径向游隙(mm)。
若无径向游隙时,单列轴承为了保持静力平衡,在各个方向上的球滚动体所受力之和与该方向上的作用载荷平衡,此时径向载荷的离散形式可表示为:
径向载荷的积分形式可表示为:
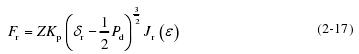
式中rJ(ε ) ——径向载荷积分系数。
利用这些积分式可计算载荷:
如图 2-6,在推力载荷作用下的角接触球轴承会产生变化,产生一个轴向的位移,根据变形几何关系可得:
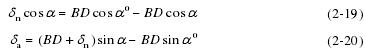
由式(2-19)和式(2-20)可得:
图 2-6 向心球轴承内外圈移动引起的球-滚道接触
式中 B ——接触体总曲率, 1o iB = f + f - ;
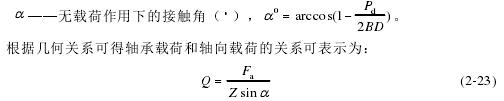
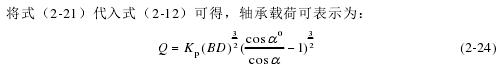
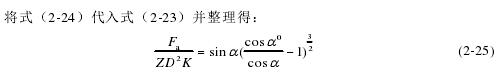

2.3.2 Hertz 接触
100 多年前 Hertz 通过简化和假设建立了研究两个弹性体的空间接触理论模型,首次对接触面附近的弹性变形使用准静态理论,并且应用于两球形体表面的接触中[50]。在分析中,Hertz 提出以下假设:
(1) 所有变形都在材料的弹性比例极限范围内;
(2) 忽略表面切应力的影响,且载荷垂直于接触表面;
(3) 接触区域的曲率半径远大于接触区域的尺寸;
(4) 接触区域的尺寸远小于接触体的曲率半径。
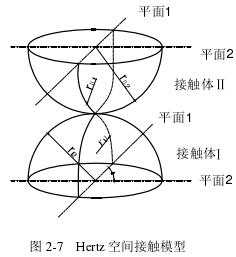
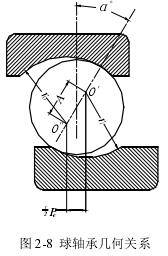
赫兹理论为坚硬紧凑的物体之间的碰撞提供了一个很好的近似值,不过理论成立的条件之一是接触区域比起碰撞体本身非常小。应用此模型假设,得到了相对精确的计算结果,就算是现在 Hertz 理论也是计算局部接触应力的主要方法。如图 2-7,两个弹性球接触时接触区域为椭圆形,图 2-8 为球轴承几何关系球滚动体和凹面体的接触模型。
说到椭圆就必须讲曲率,曲率在物理上讲是用来描述线或面弯曲程度的一个量,一般取它的绝对值表示。正负曲率应该是一个相对含义,与法线的取向有关。一般规定:凹面的曲率为负值,凸面的曲率为正值。曲率按定义分为曲率和,曲率差,这样就可以将两个物体的接触转化为一个等效椭球体与等效半平面之间的接触。凹面使接触体更加贴近,而凸面正好相反。
接触体的曲率和函数可表示为:
式中1、2——滚动体在平面 1 和平面 2 的曲率半径;
1、2——内外圈在平面 1 和平面 2 的曲率半径。
根据赫兹理论模型,轴承滚动体曲率差函数为:
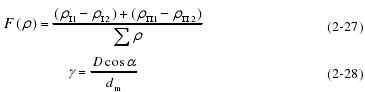
对于球滚动体在平面 1 和平面 2 上皆为凸面:
对外滚道而言(外圈两个截面皆为凹面):

所以,球滚动体与外圈之间的曲率差函数为:
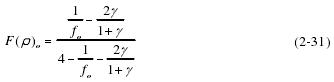
同理,球滚动体与内滚道之间的关系(内圈有一截面为凸,有一截面为凹):
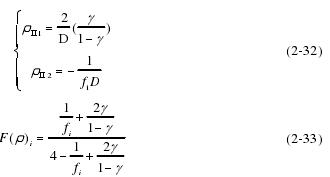
根据 Hertz 理论模型,曲率差函数是椭圆参数 a,b 的函数:

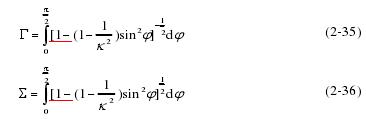
对于钢材接触体,其接触椭圆的长半轴a 和短半轴b 以及接触体远控点相对趋近量分别为:
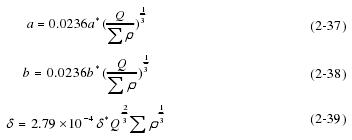



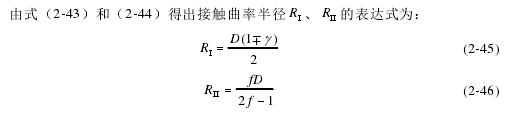
2.4 球轴承的微观几何关系
2.4.1 静载荷作用下轴承内部的变形和位移
如图 2-9 所示,根据几何变形条件可得内外滚道沟曲率中心的距离为:


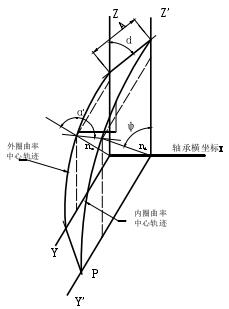
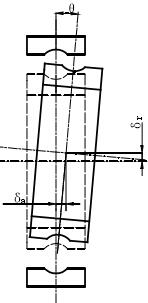
图 2-9 球轴承曲率中心轨迹 图 2-10 联合作用载荷下内圈的位移




2.4.2 静态各联合载荷作用下的轴承位移
静态载荷作用下由于陀螺力矩和离心力的影响非常小忽略不计,所以轴承变形位移不会很复杂。
如图 2-11 所示,轴向载荷与轴承变形位移的关系图中可以看出,在轴承轴向载荷的作用下,随着载荷的增加轴承的轴向位移逐渐增加,呈现正相关关系,而轴承的径向位移和角位移有所减小。在图 2-12 中,微弱的径向载荷作用下,轴承的各个方向的位移变形量基本没有变,刚度也基本不变。
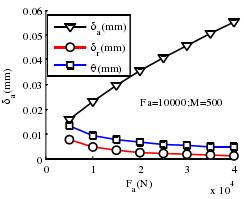
图 2-11 轴向载荷与轴承变形位移关系
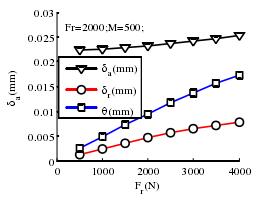
图 2-12 径向载荷与轴承变形位移的关系
2.5、本章小结
本章分析了高速电主轴的几何结构参数及其支撑轴承参数为后续电主轴的性能分析奠定了基础。分析了以角接触球轴承的宏观几何形状模型,再利用轴承的微观几何关系和微观受力状态,计算出了轴承应用中的内部载荷及其关系。但是必须知道的是,这些方法的适用范围仍然是低、中速运转的角接触球轴承。在静载荷作用下的轴承,或者是转速很低的轴承,所受到的惯性力、摩擦力和力矩等不会对球滚动体间的载荷分配产生明显的影响,因而忽略部分微小影响因素来研究静载荷作用下的球轴承。虽然如此,这些计算还是很有必要的,本章得到的数值可以作为下一章节的高速运转下的球轴承复杂的数值计算提供初始参考值,为高速球轴承的动力学分析奠定了基础。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com










