振动驱动移动机器人直线运动的滑移分岔
2017-3-1 来源：同济大学航空航天与力学学院 作者：陈祺 占雄 徐鉴
摘要:近年来，随着移动型机器人设计技术水平的不断提高，其运动形式日趋多样. 借助于仿生学的思想，模仿蚯蚓等动物的蠕动成为不少机器人设计者所追求的目标. 为了实现这一目标，学者们提出并研究了振动驱动系统. 本文研究了各向同性干摩擦下，单模块三相振动驱动系统的粘滑运动. 考虑到库伦干摩擦力的不连续性，振动驱动系统属于Filippov 系统. 基于此，运用Filippov 滑移分岔理论，分析了振动驱动系统不同的粘滑运动情况. 根据驱动参数的不同，系统运动的滑移区域被分成4 种基本情形. 对这些情形分类讨论，得到系统的6 种运动情况. 然后对这6 种运动情况进行归纳，最终得出系统一共存在4 种不同的粘滑运动，而且也解析地给出了发生这4 种粘滑运动的分岔条件. 分岔条件包含系统的3 个驱动参数，通过变化这些参数，得到了系统运动的分岔图. 借助分岔图，详细分析了随着驱动参数的变化，系统如何实现不同粘滑运动类型之间的切换，并从分岔角度给出了相应的物理解释. 最后，通过数值方法直接求解原运动方程，数值解法得到的4 种运动图像与理论分析一致，验证了系统运动分岔研究的正确性.
关键词:振动驱动系统，三相驱动，各向同性干摩擦，分岔
0.引言
众所周知，蚯蚓等软体动物通过蠕动实现运动，这种运动形式看似简单，却凭借其一大优势——无足，吸引了众多学者的关注[1-6]. 受此启发，一类新型的运动模型——振动驱动系统，近年来得到了广泛的研究[7-25]. 这种运动模型继承了蚯蚓运动的优势—— 不需要外部驱动部件，如腿或轮子，因此易于实现结构的微型化，密封化. 可以预见，基于振动驱动这一思想的机器人能更好地适应多种环境，甚至有学者期望将其制成微型胶囊机器人进入人体肠道甚至血管中治疗疾病.
2005 年，Chernousko[7] 研究了两个质量块系统的直线运动，通过选择合适的物理参数并合理地控制两个质量块之间的相互作用力，实现了该系统的最快平均速度. 在此基础上，其首次提出了由一个内部质量块和一个外部箱型刚体构成的振动驱动系统模型[8]. 在该模型中，内部质量块相对于外部箱体做周期运动，通过合理设计内部质量块的周期运动形式，外部箱体可以在内部质量块对其作用力以及支撑面对其摩擦力的共同作用下，实现周期平移运动. 因而，对质量块的相对运动形式进行设计和优化以实现系统最大平均速度是该类系统研究的一个关键问题. 纵观之前的研究，质量块的控制模式大致分为两类：对称控制和非对称控制. 对称控制意味着内部质量块的相对运动形式具有对称性，也更容易实现，比如正弦驱动，但是往往需要环境提供能使系统发生刚体位移的异性摩擦. 2012 年，Fang 等[9] 在研究三模块振动驱动系统时使用了正弦驱动，他们发现通过优化各模块中正弦驱动的初始相位差，能够有效地提高系统的稳态平均速度. 2014 年，Fang等[10] 研究了正弦驱动下，单模块振动驱动系统的运动，重点从滑移分岔的角度分析了系统的粘滑运动，加深了人们对该类系统粘滑运动的认识. 对称驱动的研究总的来说并不如非对称驱动的研究多. 早在2005 年Chernousko[7] 就提出了两种非对称驱动模式—— 两相驱动和三相驱动，对实现振动驱动系统的运动都行之有效. 2006 年，Chernousko[11] 研究了两相驱动模式，这种驱动模式下，内部质量块一个周期内的相对运动被分为两段，每段上的相对运动速度均为常数. 以实现系统的最大稳态平均速度为目标，对两相驱动参数进行了优化. 2007 年，Chernousko[12] 研究了三相驱动下振动驱动系统的运动. 该种情形下，内部质量块一个周期内的相对运动被分为三段，每段上的加速度大小为常数. 由于库伦干摩擦的存在，以及不同时间域内，内部质量块的相对加速度不同，加上系统速度的不断变化，因而系统会发生复杂的粘滑运动. 2011 年，Fang 等[13] 运用平均法研究了三相驱动的单模块振动驱动系统在不存在粘滑效应时的速度. 但是当考虑粘滑效应时，平均法不再适用，根据粘滑运动发生情况，系统运动可以被细分成8 种情况. 2011 年，Fang 等[14] 在研究两模块振动驱动系统时，在两个模块中也分别施加了这种三相驱动，通过调节两组振动的相位差实现了系统的较快运动速度. 可见，三相驱动在振动驱动系统的控制中占有重要的地位. 此外，2006 年Li 等[15] 使用的四步驱动以及2011 年Huda 等[16] 使用的四相驱动也属于非对称驱动.
除了上文中内部质量块的相对运动形式以外，另外一个对振动驱动系统的运动行为起很大影响的是系统受到的外部摩擦. 2007 年，Chernousko[12] 研究了非对称黏性摩擦下振动驱动系统的运动，这种环境模拟了系统在液体环境中的运动. 研究针对振动驱动系统速度进行了控制参数优化，并加以实验验证.2009 年，Bolotnik 等[17] 研究了平方阻尼作用下系统的运动情况，这种运动常常在系统运动速度较快、雷诺数较大的环境下发生. 研究表明，在平方阻尼作用下，即使是各向同性的阻力，系统也能实现向前运动. 2011 年，Fang 等[13] 研究了振动驱动系统在非对称库伦干摩擦下的运动情况，由于干摩擦存在，观察到了前面所述的粘滑运动.
事实上，粘滑效应至今为止仍然是振动驱动系统中的一大难题. 一方面，粘滑效应使得运动情况复杂多样，难以分析，另一方面，充分利用粘滑效应也是提高系统运动性能的重要措施. 粘滑运动往往都是在库伦摩擦之下发生，这一点，不仅在振动驱动系统中得到体现，而且在其他系统中也有发现并被研究[18;26-28]. 库伦摩擦之所以能引起粘滑运动，是因为其不连续性. 从运动状态场的角度看，这种由摩擦力引起的不连续系统，是一类典型的Filippov 系统[29-30]，而Filippov 系统最突出的就是利用滑移和滑移分岔理论巧妙地分析系统中的不连续性对运动的影响. 2010 年，Guardia 等[26]通过滑移分岔理论研究了一个干摩擦下的弹簧振子，研究证实系统存在两参数滑移分岔，并得到了其中一条余维一分岔曲线的解析表达式. 2007 年，Kowalczyk 等[27] 也通过Filippov 系统模型研究了干摩擦下的弹簧振子，发现了系统中的余维二分岔，并解释了可能发生的混沌现象. Filippov 系统理论为研究干摩擦下的弹簧振子这类系统行为，提供了重要的分析方法[18;26-28]. 受此启发，2011 年，Fang 等[10] 也利用Filippov 系统描述了非对称干摩擦下受正弦驱动的振动驱动系统，首次从滑移分岔角度阐明了粘滑效应下系统的运动情况，优化结果显示，合理优化系统驱动参数和摩擦系数，能实现系统无后退移动.
回顾振动驱动系统十年来的研究[7-25]，无论是内部驱动的设计，还是外部阻力的分类，抑或是研究方法的选用，都得到了长足的发展. 值得注意的是，绝大部分研究更多地是关注了摩擦力为各向异性时的情况，而对于同性摩擦的情形讨论较少. 因此，本文重点研究了各向同性干摩擦下的振动驱动系统的运动. 由于摩擦的各向同性，本文中将采用三相驱动这一非对称驱动以保证系统定向移动的实现. 此外，干摩擦条件下，系统的不连续性会诱发粘滑运动，这种运动的复杂性也对研究工作形成了挑战. 借助分岔理论可知，本文中所考虑的振动驱动系统也是Filippov 系统，因此可以从滑移分岔的角度对系统的运动进行分类. 这种分类有效地揭示了各向同性干摩擦下振动驱动系统多样的运动行为，对参数的设计起到一定的指导作用. 最后，我们用数值方法对理论分析得到的运动分类以及运动特性进行了验证.
1.振动驱动系统
1.1 动力学方程
振动驱动系统的基本模型如图1 所示. 系统由两个部分组成，分别为质量为M 的刚性箱体以及质量为m 的内部质量块. 由前人的工作可知，通过m相对于M 的特定振动，可以实现系统在水平直线上的定向移动，由此称其为振动驱动系统. 易知，系统有两个自由度，因而可以取两组独立的广义坐标，
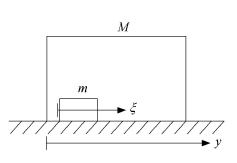
图1 振动驱动系统
由牛顿第二运动定律，可得运动方程
需要注意的是，上面的R(0) 表示速度为0 时，系统所受的摩擦阻力. 因此，如果内部振动提供的驱动力不足以克服库伦摩擦，那么摩擦力就与该力等大反向，维持系统静止状态. 如果内部振动提供的驱动力大于最大静摩擦力，那么系统有运动的趋势，此时摩擦力的大小就是最大静摩擦力. 为了简便分析，本文中最大静摩擦力近似认为等于滑动摩擦力. 所以有
式(2) 和式(3) 是振动驱动的基本力学模型.
1.2 三相驱动
假设箱体内允许质量块运动的区间长度为L
三相驱动模式的基本思想是将内部质量块一个周期的相对振动在时间上分为三段，三段区间的长度分别为r1, r2, r3. 并且，在每段时间区间内，质量块m 相对于M 均做匀变速直线运动，由式(5)r 式
(7) 易知，第一、三段中m 相对运动的加速度为正常数，第二段中m 相对运动的加速度为负常数. 一个周期内，m 相对运动的数学表达式如下
三相驱动模式下内部质量块相对运动图像如图2 所示.
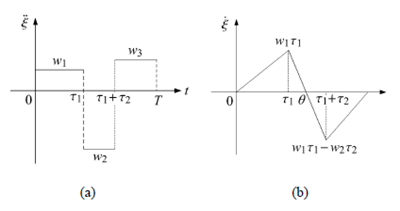
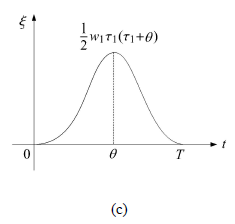
图2 三相控制模式下m 的(a) 相对加速度、(b) 速度和(c) 位移
三相驱动中，独立的控制变量有3 个，本文使用wi(i = 1; 2; 3) 作为控制的自变量. 当一组wi(i = 1; 2; 3)选定以后，其他的变量可以根据式(4)~式(6) 导出，分别为
1.3 Filippov 系统
振动驱动系统的运动情况不仅取决于内部质量块的相对振动，而且与其所受的外部阻力有关. 本文中系统所受的阻力为库伦干摩擦，干摩擦的复杂性在于其不连续性，即当系统速度方向改变时，摩擦力的变化是阶跃的. 因此，就其本质而言，本文所研究的系统，也就是式(2) 和式(8) 所决定的振动驱动系统，是一种右端不连续的微分方程系统. 这种不连续的复杂性体现在力学现象上，就是系统会发生粘滑运动，而这种特殊的运动模式又让传统的分析方法显得无能为力. 为了更好地从数学上描述运动方程，以及从力学角度更好地解释各种运动情形的发生，本文采用Filippov 系统的相关理论分析振动驱动系统. 这样做的好处是，Filippov 滑移分岔理论能有效地解释振动驱动系统中的粘滑效应. 需要注意的是，Filippov 系统中所谓的滑移运动，其实就对应了振动驱动系统粘滑运动中的黏滞状态.
采用Filippov 系统分析的步骤是：建立系统一阶状态微分方程；确定滑移区域；具体讨论在滑移区域的边界是否发生滑移分岔. 当然，由于本文中采用的驱动是三相驱动，本身也存在不连续现象，所以这又增加了分析的复杂性. 基于此，文中通过分类讨论，将振动驱动系统中可能发生的各种滑移分岔现象进行了详细的罗列、归纳.
具体地，我们首先将(2) 式由二阶非自治系统转化为一阶自治系统，即将t 作为状态变量，引入变量替换，令
式中，Hx = 0 是x 的法向量.
分界面上满足这一条件的区域称为滑移区域(sliding region)，记为? Σ. 系统只有在滑移区域上，才会发生滑移运动，也就是出现黏滞状态.根据Utkin 等效控制理论，滑移区域上的运动由两个部分构成. 一个是F1 和F2 的平均值，另一个是控制函数β(x)，该函数用来将流形拉回到与滑移区域? Σ相切，这也就保证了系统的运动始终保持在滑移区域上，具体表达式如下
2.运动分析
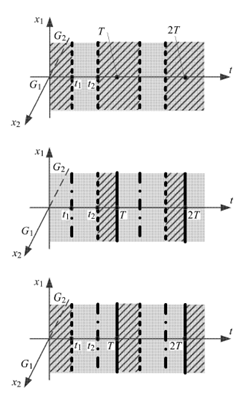
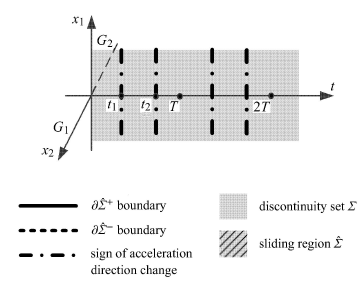
图3 系统在4 种情形(表1) 下的滑移区域示意图
表1 粘滑运动的4 种情形
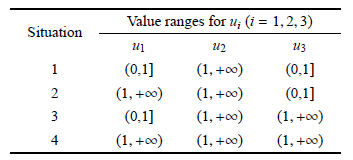
2.1 情形1
此时，由表1 中的第一行数据，等价地得到
注意到x2(t1) = 0，x2(t2) > 0，也就是可能发生滑移分岔位置的速度符号确定，因而两点处均不会发生分岔. 此时，系统的运动状态示意图对应于图5(a).
2.2 情形2
注意到x2(t2) > 0，x2(T) = 0，也就是分岔位置处速度的符号确定，因而两点处均不会发生分岔. 系统的运动状态唯一，如图5(b).
2.3 情形3
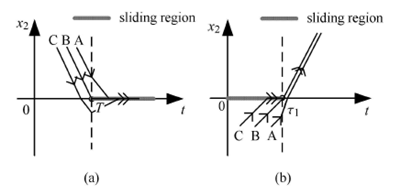
图4 系统的两种分岔示意图
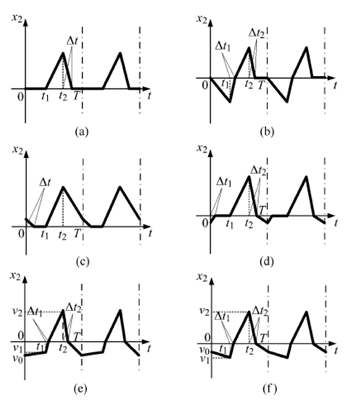
图5 系统的6 种运动形态
3 分岔
第2 节中通过对系统运动分情形进行分析，观察到系统运动出现了滑移分岔现象，也得到了6 种形式的粘滑运动. 但是需要注意的是，这并不意味着这6 种运动形式定性上各不相同. 本节将先从滑移分岔的观点分析上述各运动属于何种滑移运动类型.然后再具体分析各种不同运动发生的条件，探究随着参数变化它们之间如何通过滑移分岔实现相互切换.
3.1 归纳
Filippov 滑移分岔理论指出，右端不连续系统在不连续界面上可能会发生4 种滑移分岔(crossingsliding,grazing-sliding, switching-sliding, addingsliding)[29]，这4 种分岔的名称也可以被借用来命名滑移运动的类型. 利用图3(a)，可以看到在图5(a)中，系统从G1 空间进入滑移区域之后，并不进入G2 空间，而是保持滑移运动直到再次进入G1 空间.可以简单地理解成系统的运动状态轨迹擦过滑移区域，因而这种滑移运动称为grazing-sliding. 同样可以看到，图5(c) 中的滑移运动也可以看成是一种grazing-sliding. 这两种运动形态可以被归纳为同一种滑移运动类型.
观察图5(b)，并结合图3(b) 可知，系统由G1 空间进入滑移区域后保持滑移运动至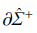
边界，然后离开滑移区域，进入G2 空间. 可以简单地理解为系统的运动状态轨迹在经过一段滑移运动之后穿越了滑移区域，因而这种滑移运动称为crossing-sliding.观察图5(d)，并结合图3(d) 可知，系统由G1 空间直接进入G2 空间，然后又回到滑移区域. 由G2 空间进入滑移区域后，系统滑移运动至
边界，最终回到G1 空间. 可以简单地理解成，系统的状态轨迹先穿过了不连续界面，然后回到滑移区域继续运动，对于这样一个具有来回转换过程的运动，形象地称为switching-sliding.图5(e) 和图5(f) 属于同一类运动，且都不发生滑移运动.
边界，然后离开滑移区域，进入G2 空间. 可以简单地理解为系统的运动状态轨迹在经过一段滑移运动之后穿越了滑移区域，因而这种滑移运动称为crossing-sliding.观察图5(d)，并结合图3(d) 可知，系统由G1 空间直接进入G2 空间，然后又回到滑移区域. 由G2 空间进入滑移区域后，系统滑移运动至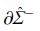边界，最终回到G1 空间. 可以简单地理解成，系统的状态轨迹先穿过了不连续界面，然后回到滑移区域继续运动，对于这样一个具有来回转换过程的运动，形象地称为switching-sliding.图5(e) 和图5(f) 属于同一类运动，且都不发生滑移运动. 图5(e) 和图5(f) 属于同一类运动，且都不发生滑移运动.综上，系统存在4 种定性不同的运动类型，其中3种运动中存在黏滞，1种无黏滞发生.
3.2 分岔图
为了更清晰地描述滑移分岔发生的条件，判断
由第二节的分析，不难发现，如果知道一个系统ui(i = 1; 2; 3) 的取值，以及P1 和P2 的正负号情况，那么系统的运动状态可以确定. 从式(26) 和式(27)可以看出，P1 和P2 的正负号情况分别与?P1 和?P2 一致，且最终只取决于ui(i = 1; 2; 3). 故而，系统的运动状态从根本上讲，取决于3 个参数ui(i = 1; 2; 3) 的取值. 由前文分析可知，随着这3 个参数变化，系统有如下4 种类型的粘滑运动.
表2 4种粘滑运动的发生条件
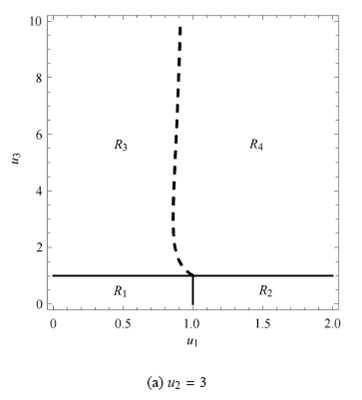
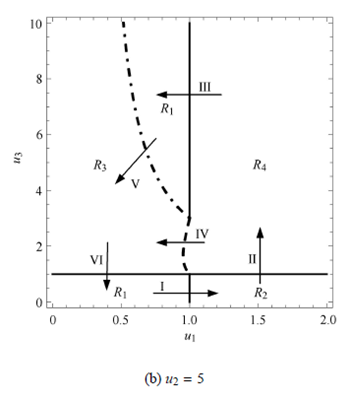
图6 振动驱动系统在u1--u3 平面的分岔图
Ri (i = 1; 2; 3; 4) 表示发生不同粘滑运动的区域，下标i 的值与表2 中的序号对应. 对比图6(a) 和图6(b)，发现图6(a) 中不存在?P1 = 0 这条线，而图6 (b) 中存在；相应地，图6 (a) 中的R1 是1 片区域，而图6 (b)中的R1 是2 片区域. 由此可知，当u2 的值较小(通过数值计算，观察到大约u2 < 3:5) 时，?P1 < 0 恒成立，看不到所谓的switching-sliding 分岔，而当u2 的值较大(大约u2 > 3:5) 时，switching-sliding 分岔可能会发生.
当u2 较大时，运动分类情况较为典型也较为丰富. 以图5(b) 为例，从左下角的R1 出发逆时针绕一圈，研究各分岔线或分界线对运动行为的影响. 从R1出发，当u1 的值增加时，系统跨过u1 = 1 分界线进入R2 (箭头I)，运动类型由grazing-sliding (图5(a)) 变成crossing-sliding (图5(b)). 这是因为随着u1 增加，系统在第一段时间上的黏滞区域逐步地变为非黏滞区域，无法再保证系统不发生后退运动. 从R2 出发，当u3 的值增加时，系统跨过u3 = 1 分界线进入R4 (箭头II)，运动类型由crossing-sliding (图5(b)) 变成无黏滞运动(图5(f)). 这是因为，随着u3 的增加，仅存的黏滞区域也逐步变成非黏滞区域，因而系统将不再黏滞. 注意到?P1 = 0 与?P2 = 0 两条曲线在u1 相交，这是因为当u1=1 时，系统在第一段上加速度为0(见式(2))，所以?P1 = 0 成立，也就意味着?P2 = 0 成立. 由此可知，从R4 出发，系统有两种选择，一种是跨过u1 = 1 进入R1 (箭头III)，运动类型再次变成grazingsliding(图5(c)). 这是因为随着u1 减小，系统在第一段时间的非黏滞区域又变成黏滞区域，因而保证系统不会后退，而且，这个区域中.P1 > 0，系统在第三段时间内会由于惯性保持速度为正，不会向后运动.另外一种，系统从R4 出发，经过.P2 = 0 分岔线进入R3 区域(箭头IV)，运动类型变成switching-sliding (图5(d))，这是因为跨过虚线，.P2 由负变正，意味着系统在第一段时间上速度由负值开始逐渐增大，且一定会在t1 时刻之前，达到速度为0. 考虑到第一段时间区间上为滑移区域，因而这会引起switching-sliding运动. 从R1 出发，跨过.P1 = 0 分岔线，系统也会进入R3(箭头V)，这是因为点划线左边.P1 < 0，意味着x2(0) < 0，而第一段时间区间为滑移区域，因而会发生switching-sliding 运动. 最后，从R3 出发，随着u3减小，系统会回到R1 区域(箭头VI). 这是因为，系统在第三段时间上的非粘滑区域变成了粘滑区域，再次保证了系统不会向后运动.
4.数值验证
由第3 节可知，决定系统分岔特性的变量是驱动参数ui(i = 1; 2; 3)，为了验证分岔结果是否正确，以及运动特性是否与理论分析一致，有必要对其进行数值计算的验证. 本节中物理参数固定，唯一改变的是驱动参数. 这里选定L = 1 m, u = 0:333 3,g = 10m/s2, f = 0:2，通过改变控制驱动参数wi(i = 1; 2; 3)，可以得到所有类型的运动特性图形. 本节中取u2 = 5，这样系统的粘滑运动类型可以由图6(b) 直观地看出. 图7 通过数值计算，得到了系统在不同区域的速度时间图. 通过比较表3 和图7，发现理论分析出的运动类型和数值计算的运动形态吻合.通过对比图5 和图7，发现运动形态的理论分析和数值计算结果吻合. 由此，验证了本文中理论分析的正确性.
表3 数值计算四组驱动参数
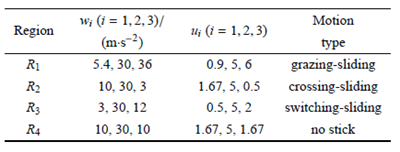
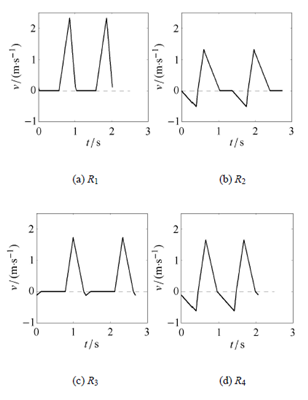
图7 数值方法得到的系统在不同区域的速度时程图
5.结论
本文研究了受三相驱动的振动驱动系统在水平面上的直线运动. 不同于以往的研究，本文重点关注了系统在各向同性干摩擦下的运动. 这种环境与物理实际比较吻合，研究工作具有潜在的实用价值.含库伦干摩擦的振动驱动系统是一种Filippov系统，因而本文采用滑移分岔的理论分析了其粘滑运动. 在只考虑系统向前运动的情况下，可以将运动分成4 种基本情形. 对4 种情形分类讨论，并加以归纳，最终得到4 种不同的粘滑运动. 借助理论分析得到的分岔条件，我们给出了在驱动参数wi (i = 1; 2; 3)变化时，系统运动的分岔图. 通过数值模拟，运动分类以及各种运动形态的正确性都得到了验证.通过本文的滑移分岔分析，可以看到，三相振动驱动系统在各向同性干摩擦环境下具有丰富的动力学行为，值得进一步的实验验证和探究. 此外，从结构上改善和提升振动驱动系统，使其更好地适应各向同性干摩擦环境，也是未来值得思考的问题.
综上，系统存在4 种定性不同的运动类型，其中3种运动中存在黏滞，1种无黏滞发生.
投稿箱：
如果您有机床行业、企业相关新闻稿件发表，或进行资讯合作，欢迎联系本网编辑部， 邮箱：skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表，或进行资讯合作，欢迎联系本网编辑部， 邮箱：skjcsc@vip.sina.com
更多相关信息
