摘要: 数控机床主轴的结构特性对其加工精度具有重要影响。根据自行设计的微型数控车床的主轴结构特征,应用有限元分析软件ANSYS Workbench 对其主轴进行了动静态性能分析。通过对微型数控车床主轴的静力分析、疲劳分析的和模态分析,得到其动静态特性参数。在静态特性分析中将轴承约束等效为刚性约束,在模态分析中将轴承约束等效为弹簧单元的弹性约束,求主轴约束模态,进而求其临界转速。求得主轴动静态特性参数均在合理的范围内,验证了主轴设计的合理性,为后续进行微型数控车床整机的动静态特性研究与优化设计奠定了基础。
关键词: 微型数控车床; 主轴; 静力分析; 疲劳分析; 模态分析
0 引言
数控机床的高精度化是其主要的发展趋势。主轴部件是数控机床最为关键的部件之一,其动静态性能对机床的最终加工性能有非常重要的影响。这一影响在刀具切削工件造成的综合位移影响中所占的比重可达到60% ~ 80%[1]。因此,随着机床速度和精度的提高,对其主轴部件的动静态性能提出了更高的设计和加工制造要求。各科研院所和研究机构对主轴部件的动静态性能进行了深入、广泛的研究[2-4]。
本文以自行设计的微型数控车床为研究对象,其主要用于加工小、微型零件,具有加工精度高,加工效率高,节约能源,占地面积少等优点。在微型数控车床的设计中,保证主轴部件具有较好的动静态特性是十分重要的,其静态特性( 包括强度、刚度和疲劳特性等) 和动态特性( 模态特性等) 的优劣都将直接影响到整台机床的使用性能。静态特性直接决定了主轴的使用性能与寿命,动态特性将直接影响主轴抵抗自激振动与受迫振动的能力,影响主轴的加工精度和工件的表面质量,从而影响微型数控车床的加工性能。为使
微型数控车床主轴具有刚度高、振动小等良好性能,需研究其主轴的动静态特性,改善其薄弱环节,减小其对机床整机的动静态性能的影响。因此,在设计阶段需对主轴的动静态特性进行合理而准确的分析,以提高设计效率,减少试验成本,进而提高其使用性能。从而对提高微型数控车床的设计水平具有非常重要的理论和现实意义。应用ANSYS Workbench 有限元分析软件对微型数控车床的主轴进行动静态特性分析。
Workbench 提供了Windows 风格的友好界面,与Solid-Works 等CAD 软件的无缝接口技术、新一代的参数化建模工具和领先的优化技术使用户能够方便快捷地进行CAE 分析。
1 、微型数控车床及其主轴结构
以自行设计的微型数控车床的主轴为研究对象。微型数控车床结构简图如图1 所示,长700mm,宽288mm,高233mm。
该机床的主轴部件结构简图如图2 所示。主轴部件设计的转速范围为400 ~ 6000r /min,可实现无级调速,总长度为216mm。主轴通过左右两组轴承安装在主轴箱内,主轴轴承采用了洛阳轴承研究所的高精密角接触球轴承,它具有膨胀系数小、弹性模量大、极限转速高和抗振动性能好的特点。左侧为单列安装的面向卡盘的角接触球轴承,型号为7003AC( α = 25°) ,起到径向支承的作用; 右侧为背靠背安装的角接触球轴承,型号为7004AC/DB( α =25°) ,承受轴向力和径向力。这样的组合保证主轴具有足够的刚度和回转精度。
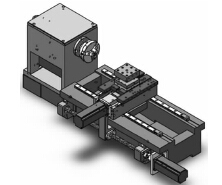
图1 微型数控车床结构图
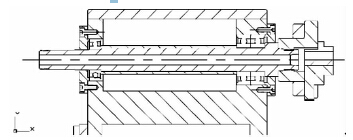
图2 微型数控车床主轴结构图
2、 静态特性分析
2. 1 静力分析
主轴的静力分析主要包括强度和刚度的计算。主轴采用40Cr 合金结构钢,调质处理,屈服强度σs =785MPa。主轴材料属性如表1 所示。
表1 主轴材料属性

施加约束和载荷时,应尽量按照实际工况进行,这样才能保证计算结果更准确。根据实际工况,加载位置有三处: 一是,主轴左侧与带轮连接的键槽,施加的是固定约束; 二是,轴承和主轴的接触,将轴承支撑简化为刚性支撑,左侧轴承用圆柱约束( Cylindrical Support)提供径向支撑,右侧轴承用圆柱约束( CylindricalSupport) 提供轴向和径向支撑[5]; 三是,切削过程中产生的切削力和转矩经过转化后加载在主轴和卡盘的连接处,但直接施加比较麻烦,因此将这几处等效为刚性单元,将车刀切削工件产生的切削力直接施加在刚性单元上,主轴输入端的转矩由负载决定,因此在主轴和卡盘结合面施加远程力( Remote Force) 模拟实际车刀切削力。这样的约束和加载方式是符合实际工况的。
根据车床切削力计算公式以及一般外圆切削实际工况[6],计算出主切削力Fc = 210N,背向力Fp = 126N,进给力Ff = 105N。在Workbench 中通过便利的远程力( Remote Force) 来模拟三个正交的切削力,设置其大小为( -105, 210,- 126) ,该远程力施力位置为实际车刀切削位置,相对主轴左端面坐标为( 350,0, 20) 。
有限元分析的仿真精度取决于有限元模型,建立模型时,忽略倒角、倒圆、螺纹等小特征,简化为多阶梯空心圆柱体。利用SolidWorks 软件完成主轴建模后,按照Parasolid 标准输出“. x _ t”文件,导入到Workbench环境下进行网格划分。在网格尺寸设置中将关联中心( Relevance Center) 设置为密网格( Fine) ,设置单元尺寸( Element Size) 为4mm,并采用默认的四面体网格进行自由网格划分。主轴模型网格划分结果如图3 所示,共有8791 个单元, 15177 个节点。
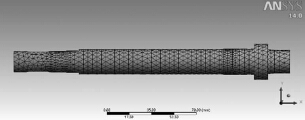
图3 网格划分后的主轴有限元模型
主轴有限元静力分析结果如图4 所示,从图4a 可知主轴最大等效应力为73MPa, 40Cr 合金结构钢的屈服强度为785MPa,安全系数大于10,即使考虑应力集中的情况,根据第四强度理论,主轴强度依然满足要求[7]。从图4b 可知主轴最大等效应变为0. 35μm。说明主轴结构在强度与刚度上均达到了较好的效果。


图4 主轴有限元静力分析结果图
2. 2 疲劳分析
微型数控车床在工作过程中,主轴旋转,所受的切削力是一个交变应力,在交变应力的作用下,虽然主轴所承受的应力低于材料的屈服极限,但经过较长时间的工作后主轴会产生裂纹或突然发生完全断裂,这种现象称为金属疲劳,故需对主轴进行疲劳分析。
在对主轴静力分析的基础上,进一步对其进行疲劳分析。S /N( 应力/寿命) 曲线是材料疲劳失效时应力幅值S 与对应的疲劳寿命N 的关系曲线[8]。设置主轴材料的S /N 曲线,如图5 所示。
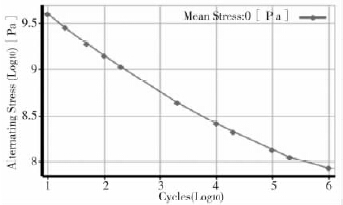
图5 主轴材料的S/N 曲线
在Workbench 的静力分析结果中添加一个FatigueTool( 疲劳工具) ,设计寿命设为1e6,进行疲劳分析,得到疲劳结果如图6 所示,从图6a 可知主轴最低疲劳寿命为1e6,从图6b 可知主轴最低疲劳安全系数为1. 181,最高为15,说明主轴设计满足疲劳寿命要求。


图6 主轴疲劳分析结果图
3 、动态特性分析
3. 1 模态分析理论
根据有限元理论,主轴的动力学方程如下:
[M]{¨x( t) } + [C]{ x( t) } + [K]{ x( t) } = { F( t) } ( 1)式中,[M]为主轴质量矩阵,[K]为主轴刚度矩阵,[C]为主轴阻尼矩阵,{ x( t) } 、{ x( t) } 和{¨x ( t) } 分别为节点的位移、速度和加速度向量,{ F( t) } 为节点所受外力向量。固有频率只与系统本身的特性( 质量、刚度和阻尼) 有关,模态分析即是求解振动系统的固有频率和振型[9]。当弹性体的动力学基本方程中的外力向量{ F( t) } = { 0} 时,略去阻尼,便可得系统的自由振动方程:
![]()

机床动态特性是影响机床性能的重要因素,将直接影响机床最后的加工性能,是评定机床性能的重要指标。对微型数控车床,其主轴的动态特性对机床的加工性能影响很大。因此,对微型数控车床主轴的动态特性分析,研究其对机床性能的影响就尤为重要。机床抵抗振动能力的大小是评价主轴动态性能的重要指标。振动的幅值与激振力的频率关系很大,对于微型数控车床,激振力的频率和振幅随着转速的提高而增大,很容易接近于系统的固有频率,当主轴的某阶固有频率与激振频率相等或相近时,将使振幅剧增,产生共振[10],因此主轴的各阶固有频率应作为主轴不可忽视的一项评价指标。
主轴的振动可以表达为各阶固有振型的线性组合,其中低阶固有振型要比高阶固有振型对轴的振动影响大,越是低阶影响就越大,因此低阶振型对轴的动态特性起决定作用,故在进行主轴的模态分析时取前6 阶低阶模态[11]。
3. 2 模态分析
为了更精确地求解主轴在实际工况约束下的模态,采用固定刚度的弹簧模拟轴承对主轴的约束,对主轴进行约束模态分析。所用求解方法为Workbench 默认的Block lanczos 法,该方法计算结果较精确,收敛较快,且计算速度也快。
轴承的预紧刚度计算十分复杂。预紧刚度越大,轴的刚性越高,但轴承寿命和最大转速减少。单个轴承预紧后的径向刚度Kr可采用式( 5) 进行计算[12]。

主轴轴承采用定位预紧方式,根据所选轴承的参数,预紧力为轻预紧,左右轴承预紧力大小分别为50N、80N。由洛阳轴承研究所提供的左右支撑轴承相关参数如表2 所示。
表2 轴承参数
根据轴承参数和预紧力以及刚度计算公式,求算得左侧轴承径向刚度为6. 359e7 N/m,即6. 359e4N/mm; 右侧轴承径向刚度值为7. 621e7N/m,即7. 621e4N/mm。
用4 个沿圆周方向上分布的弹簧模拟轴承支撑[13]。左侧为单列角接触球轴承,模拟为单组弹簧,约束在轴颈中点处; 右侧为背靠背安装的双列角接触球轴承,模拟为双组弹簧,分别约束在轴承中点处。轴承外圈全约束,即为弹簧固定端; 轴承内圈提供径向支撑,即为弹簧游动端。弹簧布置图如图7 所示。
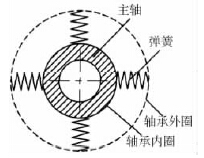
图7 弹簧布置图
在Workbench 中用Connections 中的Body-Ground中的Spring 模拟轴承支撑,Ground 对应轴承外圈,全约束,Body 对应轴承内圈,提供径向支撑。再在右侧轴承处用圆柱约束( Cylindrical Support) 提供轴向约束。输入弹簧刚度值,对主轴进行约束模态分析,得到前6 阶固有频率如表3 所示。
表3 约束模态主轴前6 阶频率

主轴前6 阶约束模态振型云图,如图8 所示。

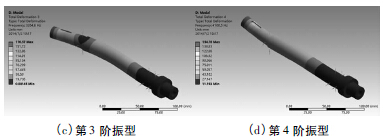

图8 主轴约束模态振型云图
从图8 可以看出,主轴为轴对称结构,第1 阶振型为主轴径向伸缩,是因为主轴大端具有卡盘定位结构,为主轴高阶振型。主轴径向伸缩对主轴与轴承的配合、间隙以及预紧具有重要影响。第2、3 阶频率很接近,振型为沿正交的两个径向方向的一次弯曲振动。
第4、5 阶频率也很接近,振型为沿正交的两个径向方向的二次弯曲振动。第6、7 阶振型应为沿正交的两个径向方向的三次弯曲振动。但主轴各阶频率太高,实际主轴达不到如此高的频率。
3. 3 临界转速
主轴在运转中都会发生振动,主轴的振幅随转速的增大而增大,到某一转速时振幅达到最大值( 共振) ,超过这一转速后振幅随转速增大逐渐减少,且稳定于某一范围内,这一主轴振幅最大的转速称为主轴的临界转速。这个转速与主轴的固有频率相关。
由约束模态分析结果可知,第1 阶固有频率为3. 3704e - 3Hz,约等于0,为刚体运动,可以忽略; 第2阶与第3 阶频率值很接近,并且振型表现为正交; 第4阶与第5 阶,第6 阶与第7 阶频率值也很接近,并且为正交振型。由于主轴设计的工作转速在6000r /min 以下,属于中低速范围,转速对主轴固有频率影响不大,所以忽略转速对主轴临界转速的影响[14]。根据主轴模态分析得到的固有频率由式( 6) 计算主轴的临界转速[15]。
n = 60f ( 6)式中: n—临界转速,r /min; f—固有频率,Hz。主轴约束模态第2 阶临界转速n2 = 60 × 3261. 3 =195678r /min,远远高于该主轴的最高工作转速6000r /min,表明设计的主轴工作转速在安全范围内,说明该主轴设计是合理的,能有效地避开共振区,可保证主轴的加工精度。
4 、结论
主轴系统是机床最为关键的系统之一,对其进行动静态特性研究对提高微型数控车床整机的性能至关重要。本文利用ANSYS Workbench 有限元分析软件建立了主轴的动静态性能分析模型,对微型数控车床的主轴进行了静力分析、疲劳分析以及模态分析,在模态分析中采用弹簧单元模拟轴承支承,得到更精确的模态分析结果。验证了主轴建模及设计的合理性,为进一步优化主轴系统结构设计提供了理论依据,为深入研究微型数控车床整机的动静态特性奠定了基础,同时也为实际试验提供了参考和依据。
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




