摘 要:为选择合理的数控车床切削用量,建立数控车床切削参数能量消耗和加工效率数学模型。在切削参数能量消耗估算模型中,通过实验拟合与正交实验分别获取数控车床的空载功率和切削功率函数,进一步给出数控车床切削阶段能量消耗函数。在车床加工条件的各种约束下,设计了一种基于多目标教与学优化算法来求解切削参数能量效率优化模型,以切削阶段加工能量最小和加工效率最高为目标,获得切削参数优化的Pareto前沿解,并采用层次分析法建立了切削参数的决策模型,较客观地选取了更优车削参数组合。通过数控车床实例优化验证了所提策略的可行性和有效性。
关键词:车削;能耗;切削参数;教与学优化算法;数控车床
0 引言
数控技术是当今先进制造装备行业的核心技术,在数控加工过程中合理选择切削参数可节约能耗和资源、提高生产效率,从而提升企业经济效益、增强竞争力。然而,目前我国多数数控加工企业还在凭经验、参考手册、通过试切来选择切削参数,往往难以实现能量效率的最优化。随着现代智能优化算法、切削理论、数学建模和模型分析方法的不断发展和完善,通过优化切削参数来提高加工效率、减少能量消耗已成为研究的热点。
对于切削参数优化问题,国内外采用较多的智能优化算法有模拟退火算法[1]、遗传算法[2]、粒子群优化算法[3]等。也有众多学者在此基础上对以上算法进行了改进,例如:CHEN 等[4]在车削参数优化问题中,将Hooke-Jeeves模式搜索与模拟退火算法进行了结合;SRINIVAS等[5]提出了惯性系数随迭代线性减小的粒子群优化算法来解决车削参数优化问题;SARAVANAN等[6]以最小生产成本为目标,利用模拟退火算法和遗传算法对车削的切削用量进行了研究;谢书童等[7]提出了基于边缘分布估计的优化算法,分别采用基因修复与惩罚函数两种策略解决车削参数优化问题。另外,在切削参数优化模型上也有新的研究,除了将加工成本和工时作为优化目标外,更关注机床的能耗研究,例如:YAN等[8]建立了以能耗、生产率和切削质量为多目标的铣削参数优化模型,首次将切削能耗考虑在内,利用灰色关联分析和曲面响应法对其进行了寻优;李聪波等[9]利用复合形法,以高效低碳为多目标进行了切削用量的寻优,并通过实例验证了模型的有效性;李建广等[10]紧接着也从能量消耗的角度对切削参数进行了优化,考虑了机械加工对环境的影响。可见,机械加工切削参数的能量效率优化研究已经越来越受到研究者的重视。
当前,求解切削参数优化的问题大多采用元启发式优化算法,然而这种算法的参数设置对求解结果有较大影响。近年来,一种高效、可屏蔽参数干扰的教与学优化算法受到研究者的广泛关注;基准函数实例测试显示,该算法比遗传算法和粒子群优化算法能获得更高质量的解[11]。本文首先通过正交实验给出数控车床切削阶段的能量估算函数,设计一种改进多目标教与学优化算法解决切削参数的能量效率优化问题,采用层次分析法选择更合理的切削参数,实现切削用量从定性的随机选取到定量选取,并通过实例优化验证了所提策略的可行性。
1、 数控车床能量效率模型
在数控车床切削过程中,切削三要素是影响加工过程能量效率的关键因素。为减少加工能耗、提高加工效率,选择合理的数控车床切削用量,建立数控车床切削参数的加工能量和加工效率数学模型。
1.1 加工能量数学模型
数控机床加工过程涉及待机状态、空载状态和切削状态,由刘飞[12]等对机床的研究理论可知,当系统处于切削状态时,机床的总功率损耗包括空载功率损耗Pu、切削功率损耗Pc和附加载荷功率损耗Pa。目标函数是优化变量的函数,是评价和选择优化切削用量的指标。本文所考虑的机床加工过程的功率损耗均与切削三要素有关,故第一个目标为:
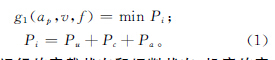
在机床运行的空载状态和切削状态,机床的空载功率均对机床的功率损耗有较大影响。同样地,刘飞等[12]指出,只有当机床空载功率与主轴转速n近似呈二次函数变化关系时,才能准确地反映其损耗功率的构成,机床空载功率可通过实验拟合得到:
![]()
对于负载时的附加载荷损耗功率Pa,其附加损耗机理十分复杂,一般无法通过理论计算准确获得其函数关系,刘飞等[12]指出其附加载荷损耗与载荷损耗呈近似的线性比例关系,比例系数α 的取值范围一般为0.15~0.25。

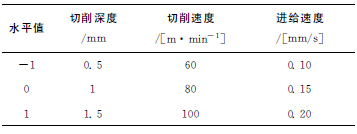
通过正交实验设计可以获得切削功率与切削参数之间的指数经验模型关系。采取三因素三水平正交实验设计,每个切削参数被编码为-1,0,1三个水平,分别按式(5)进行编码,对式(4)取对数简化后,可以得到切削参数和响应值的编码关系(式(6))。
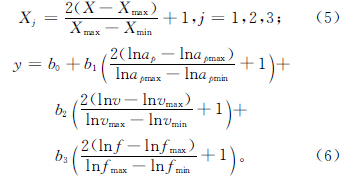
对上式进行变量分离,可得到系数和指数关于回归系数bi(i=0,1,2,3)的代数式,而4个回归系数可根据矩阵原理计算求出:
![]()
式中:X 为切削参数的编码矩阵,A 为对角阵,B 为回归系数矩阵,从而可以通过矩阵原理求出切削功率Pc指数模型中的各项系数和指数,得到总加工能量的数学模型。
1.2 加工效率时间数学模型
切削时间即为加工时间的一部分,均可反映机床的加工效率,即加工时间短、机床的生产率就高,在保证加工质量的前提下,这也是现阶段各数控装备企业追求的目标之一。其中加工工时可以分为实际切削时间、换刀时间以及辅助时间三部分,其准确表达式为:
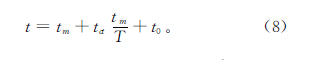


1.3 约束条件
切削用量的取值受诸多因素约束,主要有切削参数自身的范围约束、机床性能约束和加工质量约束等,数控车床的切削参数只能在约束条件的范围内进行寻优。
(1)机床切削速度约束
主轴转速必须在机床允许的最小转速和最大转速之间,而转速与切削速度之间可相互转换。对某一特定数控车床而言,其正常转速有一个具体范围,当加工工件的直径D 确定时,可以得到切削速度的范围:

(3)机床背吃刀量约束
背吃刀量取决于刀具材料、工件材料和车床允许的最大切削力。背吃刀量也与加工工艺有关,一般地,进行粗加工的背吃刀量相对较大,但加工表面无要求。本研究中对加工表面有较高要求,故背吃刀量的选择在半精加工的范围内取值:
![]()
(4)机床功率约束
加工过程所消耗的功率必须在机床所能提供的最大有效切削功率范围内。最大有效切削功率Pcmax直接受机床主电机功率约束,机床主电机功率和机床的传动系数η则由数控车床决定:
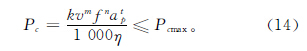
(5)切削力约束
加工过程中刀具与工件接触,所产生的切削力需进行约束。其中:主切削力最大,背向力和进给力均小于主切削力,主切削力必须在最大允许切削力范围内,其值可通过查表获取:
![]()
(6)表面粗糙度约束
切削用量直接影响已加工表面的粗糙度,优化的切削用量也必须满足表面粗糙度的约束。粗糙度可按加工要求获取,刀尖圆弧半径rε由车刀决定:
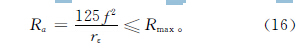
综合以上目标函数和约束条件,得到该数控车床切削参数的多目标优化数学总模型:
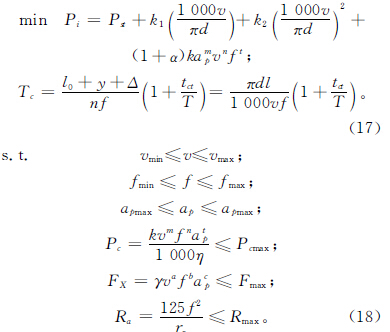
2 、多目标教与学算法求解切削参数优化问题
2.1 改进的教与学算法
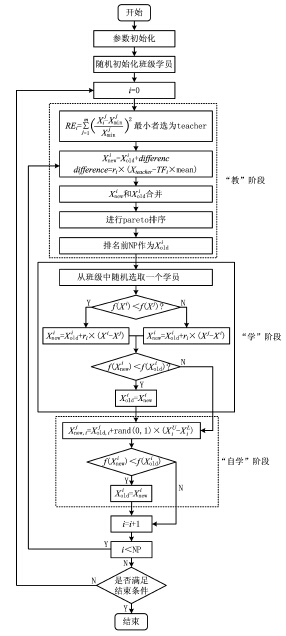
教与学优化算法是Rao等于2010年提出的一种新的群智能优化算法,该算法的参数少、操作简单、易理解、求解速度快、精度高且具有极强的收敛能力[11]。本文设计了一种改进多目标教与学优化算法,以解决切削参数能量效率优化问题,算法求解过程如下:

(2)教阶段 首先根据设定的最小偏优策略在学生群体中选取一位老师Xteacher,然后班级中每个学员根据Xteacher和学员各科目的平均值mean之间的差异性进行学习。
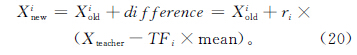
式中学习步长ri=rand(0,1)。考虑到在实际学习时,学员根据自己的接受能力向老师学习,学习能力强则学习较快,学习能力弱则学习较慢[13],因此教学因子采取自适应的模式为:

(4)自学阶段 在实际中最主要的学习方式是自学,是自己和自己比较,增加自学方式可以使学员的学习形式更加多样化,从而使算法的全局搜索能力更强,其自学方式为:
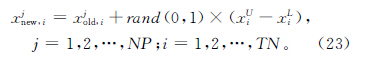
2.2 切削参数优化过程
班级中学员数为种群大小NP,学员需要学习的科目为切削三要素,即任务数TN=3。目标函数为学员的学习成绩,作为切削参数选取的重要指标。对于模型中约束的处理,在学员初始化时,首先在切削三要素范围内随机生成班级学员的科目值,缩小寻优范围。对于主切削力、最大切削功率以及加工质量的约束,在教、学以及自学阶段结束后进行过滤处理,对于过滤后的学员,其切削三要素重新在约束范围内生成,重构班级学员。
非支配解集的构建是通过Pareto排序实现的,设定一学员的加工能量和加工效率均小于另一学员才被该学员支配,否则为非支配解。然后对非支配解进行排序,得到排序为1的即为非支配解集,该解集中的任一学员均不被其他学员支配,而所寻求的多目标最优解在其构成的Pareto前沿解集上。
在教阶段,首先对初始解进行约束过滤处理,然后进行Pareto排序,学生向老师学习,需要找出一个Xteacher。本文的研究目标是对切削参数进行寻优,要求需同时满足机床功率损耗和切削时间达到平衡状态的较小值,因此,算法加入了最小偏优策略进行改进,即学员各科目成绩与对应的全班各科目最优成绩的偏离总和最小的学员作为学习对象。对于Pareto排序为1的学生,计算每个学生的目标值和最小目标值的相对误差平方和:

教学工作完成后,将得到同样多的新学生,这些学生中理论上存在比之前更差的学生,然后合并新学生和旧学生的成绩,统一排序后,取成绩排名为前班级人数的成绩所对应的学员作为新的学生群体。在学阶段,从班级中随机选取一个学员进行相互学习,若成绩提高则替换,否则继续保留原学员。自学阶段和学阶段类似,只是学习对象有所不同,此时学习对象变为自己,学习的过程相同。结合本文的研究目标,改进的多目标教与学优化(Teading-Learning-Based Optimization,TLBO)算法实现的流程图如图1所示。
3、 优化实例验证
3.1 切削能量模型实验与验证
3.1.1 空载功率拟合
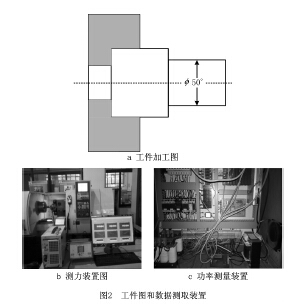
通过CK60数控车床配备华中数控系统进行切削加工实验,工件(45#热轧钢)切削长度为100mm,直径为50mm,如图2a所示;采用Kistler测力仪以及NI虚拟仪器采集切削力信号(如图2b),可获得三向切削力大小,车刀采用主偏角45°的涂层硬质合金刀具MSSNR2525M12;另外,待机功率和空载功率均由WB9128三相功率传感器测取,如图2c所示。
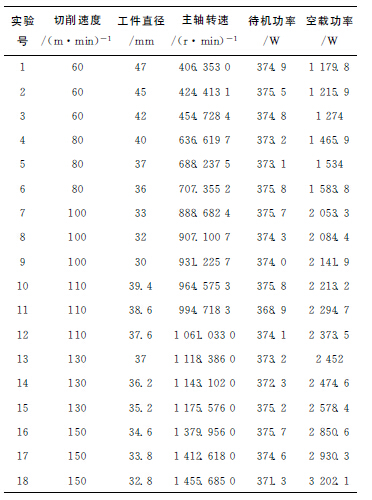
为研究机床空载功率和主轴转速的关系,进行了18组实验,转速为145r/min~1 500r/min,主要根据不同切削直径对应的切削速度转化而成。切削的同时,功率传感器采集主轴转动前后的信号,得到如表1所示的待机功率和空载功率。
表1 空载功率实验数据
用MATLAB进行二次拟合,得到如下空载功率与主轴转速的二次关系式:
![]()
从拟合结果中不难看出,转速二次项对空载功率损耗的贡献系数较小,可见在该实验条件下,空载功率基本与主轴转速呈线性关系。对其进行方差检验R2=0.98,F=373>F0.05(2,15),拟合效果甚佳。另外,最低空载功率即为转速为零时的功率,与试验中的待机功率非常接近,进一步说明该二次拟合的准确性,因此关于主轴转速的二次型可以有效且准确地预测相应的空载功率损耗。
3.1.2 切削功率估算
切削功率可以通过扭矩传感器或者测力仪间接获取,本实验采用Kistler测力仪以及NI虚拟仪器采集切削力信号,测取X 和Z 向切削力,由下式间接获取切削功率,其测力装置如图2b所示。
![]()
由于三因素均对切削功率有较明显的影响,若采用普通实验,则需大量的数据才能得到较好的结果。本实验采用三因素三水平的正交实验设计,其正交试验结果如表2所示,表3为对应的参数编码。
表2 正交试验表
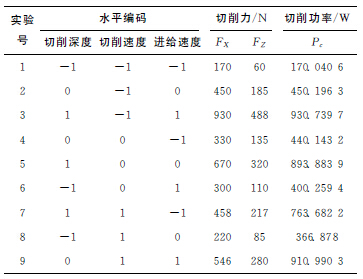
表3 各水平值对应的参数设置

同理,为了总模型中主切削力的约束,主切削力FX的指数模型如下:
![]()
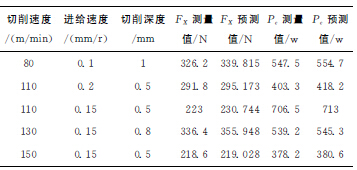
另外,进行了5组实验来验证以上模型,结果如表4所示,其中主切削力FX的预测误差为3%,而实际切削功率的预测误差仅为1.5%,二者均在误差可控范围之内,所得模型具有较高的预测精度。
表4 模型验证实验数据
因此,结合以上在实验基础上获取的空载功率和切削功率模型,切削阶段总能量模型如下:
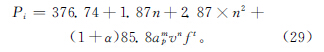
3.2 切削参数能量效率多目标优化
3.2.1 切削参数优化
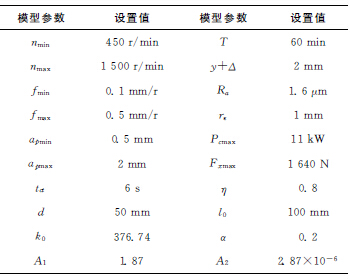
改进的TLBO算法使用C++语言编译,运行于Windows 7操作系统,单核英特尔酷睿CPU,2GB内存。其模型中的各参数设置如表5所示,算法中的种群大小NP=50,最大迭代次数为200代。
表5 模型参数设置表
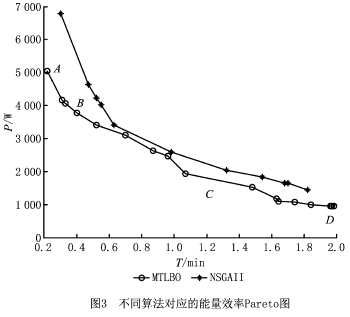
该算法最后得到了17组Pareto前沿解,其中第1组和第17组分别具有机床功率损耗最小和切削工时最小的两个极限值,其他均在二者之间,无传统意义上的最优解。为证明改进的TLBO算法具有更优的效果,将其与经典多目标进化算法快速非支配排序遗传算法(Non-dominated SortingGenetic Algorithm,NSGAII)进行了比较,在同样的种群大小和迭代次数下,NSGAII得到了11组非支配解,非支配解的分布也不及改进的TLBO算法。另外,其Pareto前沿均在本文所提出的改进的TLBO算法之上,而目标为机床功率P 和加工工时T 均取小值,故NSGAII得到的Pareto解均被其支配,这表明了改进的TLBO算法在得到最优解方面表现出了很强的搜索能力,其Pareto图如图3所示。在此曲线上的点均可作为较优解,后文将用层次分析法进行决策,得到折衷最优的切削用量。
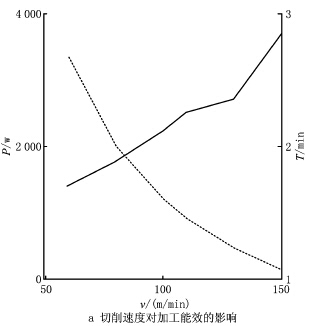
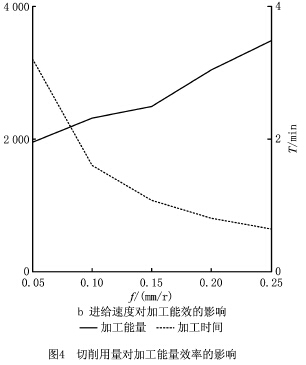
3.2.2 切削用量对加工能量效率的影响分析
切削用量是影响加工过程能量效率的重要因素,当f=0.1mm/r和ap=0.5mm时,切削速度对加工能量效率的影响如图4a所示,随着切削速度的增加,切削阶段的能量消耗不断增加,加工时间不断减小。当v=100m/min和ap=0.5mm时,进给速度对加工能量效率的影响如图4b所示,随着进给速度的增加,切削阶段的能量消耗不断增加、加工时间不断减小。可以看出,二者对切削阶段的能量消耗和加工时间的影响趋势一致。当然,当切削速度和进给速度一定时,随着背吃刀量的增加,切削力增大,导致切削阶段消耗的功率增加,而加工时间长短和背吃刀量无关。然而,在选择车床切削用量时,切削三要素之间具有内联性,当背吃刀量增加时,为防止切削力和消耗功率过分增加,必然会影响进给速度和主轴转速的选取,从而影响加工时间的长短。
3.3 切削参数决策分析
3.3.1 切削参数选择
为了在17组Pareto前沿解中找出最优的一组解,采用层次分析法决策,将这17组解作为方案层,将两个目标函数所得的值作为准则层,采用层次分析法的目标就是确定一种最优参数组合,即目标层。该方法将定量分析与定性分析结合起来,利用决策者的经验,采用1~9的标度判断各衡量目标能否实现的标准之间的相对重要程度,并合理地给出每个决策方案的标准的权数,利用权数求出各方案的优劣次序,从而选择出更优的切削参数组合。
由Pareto图可以看出,机床功率损耗和实际切削工时是一对互逆的准则,不可能同时达到最优,若要得到一组相对更优的解,应该对其折中取值。因此,将Pareto解集曲线进行分段,对BC段的6组参数采用层次分析法进行决策。
按照判断矩阵元素的标度方法可以得到方案层对准则层的成对比较矩阵P 和T 以及各矩阵所对应的最大特征值分别为6.122 5和6.273 2。

将机床功率损耗与实际切削工时进行对比,显然机床功率损耗比实际切削工时对方案的选择影响大,因此取其稍微重要,即有准则层对目标层的权向量W2=[0.75,0.25]T,其一致性指标CI=0,通过一致性检验。另外,求出P 和T 的最大特征值对应的特征向量后,归一化处理即为各方案对各准则的贡献程度,即方案层到准则层的权向量W1,最后得到层次总排序W,
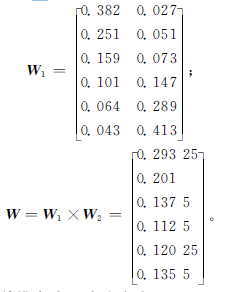
层次总排序的一致性检验:CR=0.026<0.1,通过一致性检验,可以得到第9组的权重最大,即综合考虑两个目标且满足各项约束条件时,第9组的参数组合相对最优。
3.3.2 结果分析
当切削直径为30mm的工件时,将第9组最优切削用量组合按机床转速表和进给量表规范得到转速n=900r/min,进给量F=170mm/min,ap=0.5mm,进行实验验证最后得到机床功率损耗为1 964W,实际加工时间为65s。由切削原理可知,由于半精加工时切削深度较小,产生的切削力也较小,可在保证表面粗糙度的前提下适当加大进给量,可以看出改进的TLBO算法在多目标优化中应用的结果符合切削参数的选择原则。因此,采用本文所提改进的TLBO算法可以有效地选择出切削用量。
4 结束语
为合理选取数控车床切削用量,本文建立了数控车床的加工能量效率模型,采用改进的基于Pareto排序的多目标TLBO算法进行寻优,对Pareto前沿解采用层次分析法进行决策,得到了最优切削参数组合。可以看出,合理切削用量的选取受到机床自身多个因素的影响以及加工要求的约束,通过分析切削参数对机床加工能量以及加工效率的影响,切削用量的选取具有内联性。本文主要针对数控车床车削加工切削参数能量效率优化,对数控机床能耗的影响分布以及多源能量流特性的研究将是未来的重点研究方向。
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




