摘要: 为了提高冲压模具设计时计算非标锻件备料尺寸的效率，提出了一种冲压模具非标锻件备料尺寸的快速计算方法。将三维锻件模型的表面离散为三维点阵，利用QuickHull 算法计算三维离散点阵的最小凸包; 以凸包的各表面为基准，通过投影和二维凸包算法计算包容盒，通过比较获得最小的三维包容盒尺寸。该算法计算的包容盒虽然不是锻件几何体在理论上的最小包容盒，但针对这类非标锻件来说，其计算精度和计算效率能够满足冲压模具结构设计时的备料需要。

       关键词: 冲压模具; 非标锻件; 备料尺寸

      汽车覆盖件模具中的非标镶块大多数通过锻造工艺制造，例如: 修边镶块和翻边镶块数。锻造坯料是根据镶块实际大小采购的长方体或圆柱体钢块，而镶块一般都是不规则的形状。为了确定采购坯料的尺寸，使其既能加工出所需要的零件，又使下料最省，达到提高材料利用率、节约成本目的，因此产生了确定最小坯料问题。确定最小坯料问题是典
型的解决“最小包容盒”问题，由于实际使用时并不追求理论上的最小值，只需求得近似最小包容盒，并且要求计算耗时少，因此计算冲压模具非标锻件坯料尺寸可以认为是一种求解近似“最小包容盒”问题。

      Freeman H 等 证明了凸多边形的最小包容矩形必须有一条边与凸多边形的一条边共线。MartinＲ Ｒ 等 的算法用于处理如一个二维或三维物体能否放入一个方形盒子中，也就是求物体的最小包容盒。证明任意多边形的凸包最小包容盒等价于多边形的最小包容盒。

     Chan C K 等 提出了确定任意实体最小包容盒算法，该方法通过将实体投影到3 个主平面，然后通过分析投影轮廓来简化复杂的三维问题。轮廓的方位是在指定的范围中旋转它们来确定，然后通过这些方位估算具有最小包容盒体积时实体的方位。该方法当被测实体较复杂时，旋转、投影和计算轮廓面积的耗时都会相对较多。

      颜建军等 基于遗传算法和粒子群算法，通过旋转包覆实体的正方体来确定实体的最小包容盒。如果零件越复杂，旋转和迭代次数越多，相对计算时间较长。

     上述最小包容盒计算方法精度高，但由于旋转迭代，计算时间较长，难以满足冲压模具非标锻件备料的快速近似计算要求。

     1 、基于凸包算法的包容盒计算方法

     本文需要解决的问题是快速计算冲压模具非标锻件备料尺寸，用于采购坯料进行加工生产。由于坯料尺寸一般为整数，故计算的备料尺寸精度要求近似最小即可，因此本文提出了一种快速计算三维实体的近似包容盒算法。该算法利用Martin Ｒ Ｒ 等的证明结论“任意多边形凸包的最小包容盒等价于多边形的最小包容盒”。首先将三维实体离散得到
表面的离散点集，然后通过离散点集求取包容盒的最小凸包，该凸包同时也是三维实体的最小凸包，最后通过凸包计算包围它的近似最小包容盒。本算法过程主要包括三维实体表面离散成点集、求解点集的最小凸包模型、求解凸包模型的包容盒等几个部分，包容盒算法如图1 所示。

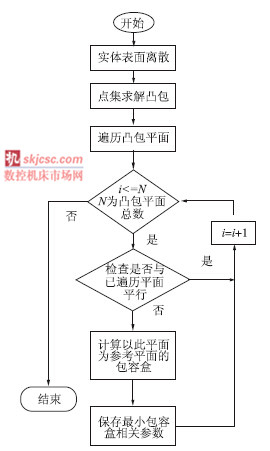
                  图1 包容盒算法流程图

     1. 1 三维实体表面离散

  
     算法首先需要对三维实体进行离散。离散点的数量会影响后续计算的效率和计算准确性，同时离散精度会影响离散点数量和表示三维实体的精确性，因此需要选择合适的离散算法和离散精度等。包容盒是三维实体的整体尺寸，三维实体的内部结构对此并没有影响，离散实体时只需要离散实体的表面。本文选择的离散算法主要通过弦高、步长和角度3
个参数( 图2) 来控制离散精度和离散点数量。对于实体中的平面，如果平面的顶点都在包容盒内部，那么该平面一定也在包容盒内部，故平面只需要其顶点表示即可，因此离散时可以考虑将步长参数设为无限大，这样可以减少离散点数量。

      
  
                        图2 三维实体离散参数示意图

      1. 2 离散点集的凸包模型

     一个由点集P 构成的凸包就是包含P 自身在内的所有凸集求交集的结果，也就是包括点集P 的最小的凸集，如图3 所示。

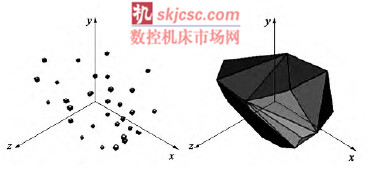
                          图3 三维点集的凸包示意图
 

     目前已存在较有效的求解三维点集的凸包算法，如Chand Ｒ Chand 和Shan S Kapuer 的“礼物包裹”( gift wrapping) 算法［5］、Preparata F P 和Ｒivest Ｒ 提出的分治算法［6］、Bradford Barber C 和David P 的QuickHull 算法［7］、Tang M 等［8］的GPU 加速凸包计算方法、毛鹏的改进快速凸包算法［9］以及Kim 等的任意几何体凸包计算方法［10］等。本文采用Quick-Hull 算法求解离散点集的凸包，该算法属于随机增量算法，通过动态地添加外部点来逐步构造出完整的凸包，该算法较容易实现，并且时间复杂度也达到了下界O ( nlogn) 。

     1. 3 凸包模型的近似最小包容盒

    凸包每个面均由三角形组成凸多面体。包容盒是包裹该凸包的一个长方体。理论上讲，凸包最小包容盒的面可能与凸包所有平面都不平行，但是为了达到快速求解近似最小包容盒目的，本文所求的包容盒平面与凸包某一平面平行。当实体越复杂时，上述方法得到的包容盒与理论上最小包容盒会越接近，恰好符合非标锻件表面较复杂情况。因此，以
凸包某平面为基准平面，将凸包所有顶点法向投影到该平面上，其中与该基准平面最大的垂直距离就是包容盒的高度。投影点在基准平面上形成了新的点集，这样问题就转换为求二维点集的最小包容矩形。

      二维点集最小包容矩形的求解分为两步( 图4) : 第1 步是求解二维点集凸包，目前有较多有效算法可解决此问题，如Javis 卷包裹( Wrapping) 算法、Graham 扫描算法、周德培的Z3 － 1算法和Z3 － 2算法等，本文采用Graham 扫描算法来求解二维凸包;第2 步是求解二维凸包最小包容矩形，根据Freeman等的证明“凸多边形的最小包容矩形必须有一条边与凸多边形的一条边共线”，故可以将凸多边形顶点投影到某条边上，包容盒高度就是所有顶点与该边之间的最大距离，包容盒的长度就是所有投影点之间的最大距离，这样就能得到与该边共线的包容盒面积，循环计算每条边就能得到最小包容矩形。

     通过投影点集的最小包容矩形和包容盒的高度就能得到与该平面平行的包容盒的体积，循环遍历所有凸包的面，就能得到近似最小包容盒。

      2 、应用实例

     本文在CATIA 平台上实现了提出的快速冲压模具非标锻件备料尺寸计算算法，并以某汽车覆盖件模具的冲孔斜楔( 图5) 为例进行实例分析。通过实际使用发现，对于锻件类零件，该算法相较于传统方法在不影响计算精度的情况下能够显著提高计算效率。图6 是计算结果显示( 其中，显示的尺寸是向上圆整的) 。

      
  
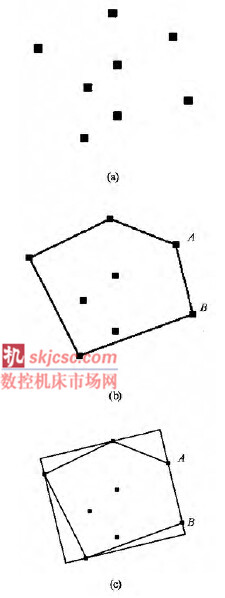
         图4 二维点集最小包容矩形求解示意图

      
  
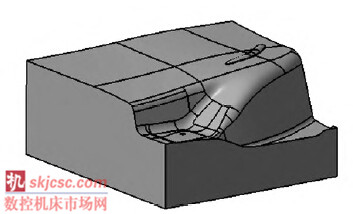
                                 图5 实验算例

       
  
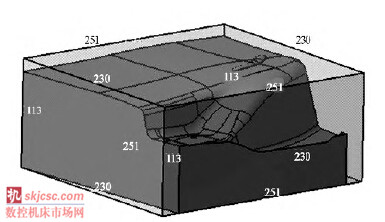
                                 图6 计算结果示意图

     一般而言，影响冲压模具非标锻件的计算效率和精度的是非规则型面，因此离散参数的选择对计算时间有较大影响。离散参数弦高与角度越小，离散点就会越多，所求最小凸包的三角形面就会越多，计算耗时就会越多。但是在实际模具设计生产过程中，采购的锻件坯料尺寸为整数，对计算结果需要进行圆整处理，提高离散精度计算的精确值可能并不会影响圆整后的结果。如表1 所示，提高离散精度后计算时间会增加，但是结果并没有影响。因此，可以通过适度放大离散时的弦高和角度参数提高计算效率。

  
                              表1 实体离散参数的影响

     快速计算方法在CATIA 平台上进行了计算验证，并通过实际使用中也证明了该算法的计算精度能够满足实际备料需要。对于常见的非标锻件，该算法的计算时间在0. 4 s 以内，并且能够通过适度放大离散参数来提高计算效率。

     本文提出的算法不仅适用于冲压模具非标锻件的备料尺寸计算，而且对其他复杂零件的包容盒计算也有较好的效率和精度。

     3 、结语 

    本文根据非标锻件的特点和设计人员对备料快速与近似精确的要求，提出了快速计算备料尺寸的算法。该算法首先离散被测实体，然后根据离散点计算最小凸包，最后计算凸包的近似最小包容盒。另外，该算法允许指定加工面，即坯料的某个面与指定的加工面重合，实质是将三维问题最小包容盒问题转换为二维最小包容盒问题，计算效率和精度更高。在实际使用中也证明了该算法的计算精度能够满足实际备料需要。