基于SYNTEC的螺旋锥齿轮加工机床数控系统开发（上）
2017-1-3 来源：沈阳工业大学 作者：张西栋
摘要
SYNTEC-10B 数控系统是台湾新代科技股份有限公司研发的一款具有较高性价比的产品，该数控系统具有很好的开放性，是数控系统二次开发的良好平台。弧齿锥齿轮数控加工涉及到的参数较多，齿轮规格调整后需要重新编制加工程序，而且数控编程不直观，人机交互性差。为了解决不同弧齿锥齿轮加工的数控编程的繁琐性问题，提高加工效率，利用 e HMI 软件对 SYNTEC-10B 数控系统的人机交互界面进行了客制，使其能够通过屏幕界面直接输入弧齿锥齿轮的基本参数的形式，即可生成相应的数控加工程序，完成自动化加工。
对螺旋锥齿轮的啮合原理以及加工过程进行了分析，对相对微分法、啮合方程的确定、等距共轭原理以及第二共轭曲面的确定等内容进行了描述。分析了螺旋锥齿轮的加工原理和方法、局部共轭原理及齿面数学模型的建立，为后续界面的开发提供了理论基础。
利用 e HMI 软件对弧齿锥齿轮加工过程中参数输入、模拟仿真等相关界面进行了客制与设计。搭建了客制化界面系统的整体框架图以及弧齿锥齿轮加工系统的人机界面的工作流程图。通过建立专案，添加相关画面档与功能键的形式对整个人机界面进行了客制。设计制作了齿制选择、加工参数输入、刀具参数输入等主要画面档，将齿轮加工所需要的各种参数信息通过不同组件的形式添加在画面档上，使相关的参数输入界面简洁明了，便于机床操作者进行相关的数控编程。
为了配合画面档的切换、参数输入等动作，相应地客制设计了与各级画面档相对应的功能键。通过测试仿真模块，对开发的多窗体界面中的各级画面档与功能键相关客制工作进行了仿真检测，确保了各种参数的正确性。通过整个分析设计过程，最终达到参数的输入、加工代码的生成、加工仿真程序的运行整个过程的人性化和快速化。
构建了人机界面的各层级关系框图，使界面之间的层级关系一目了然；按照操作习惯对数控系统轴群显示界面进行了设置。基于客制的要求，通过搭建架构图的形式对客制过程中的新代数控系统内装型 PLC 进行了总结。将 R 寄存器中允许操作者读写的地址分配给客制过程中的各输入变量，最后将客制的专案进行了软件封装。
关键词：新代数控系统，螺旋锥齿轮，画面档，测试仿真
第 1 章 绪论
1.1 课题来源及研究背景
1.1.1 课题来源
基于课题组的科研项目《大型螺旋锥齿轮专用数控机床的开发》，提出了本课题。该科研项目是沈阳市科技创新专项资金—工业科技攻关专项（F15040200）支持的项目。项目中的数控机床采用的是台湾新代科技有限公司开发的，具有较高性价比的SYNTEC-10B 数控系统；该系统操作简单，开放性较好，能够满足弧齿螺旋锥齿轮加工的基本要求。为了提高数控系统的人机交互性，适应不同生产批次的零部件加工要求，满足数控机床普通操作者的操作要求，对 SYNTEC 数控系统人机界面进行专用化地客制。
1.1.2 课题研究背景
计算机作为 20 世纪人类最伟大的科技发明，推动了整个社会的变革。计算机技术以及相关的控制技术在机械制造领域中的应用促使制造行业生产形态发生了重大转变。1952 年美国推出了世界上第 1 台数控铣床，至今已经过了 60 多个年头，在这段时间里，车床、磨床、铣床、冲压床、电加工机床、镗床、加工中心以及各类专用机床慢慢发展起来，逐渐形成一个完备的数控机床家族体系。数控系统经过半个多世纪的发展，先后经历了硬件数控和软件数控两个发展阶段[1] 。
1952 年发展起来的电子管类数控系统开启了硬件数控系统阶段，该类数控系统是这一阶段的第 1 代。由于硬件的限制，早期计算机运行速度较低，不能满足数控加工实时控制的要求，为此，技术人员将数字逻辑电路嵌入到一台专用计算机中，组成数控装置，这种数控装置即为硬件连接数控，简称数控（NC）。 1961 年以晶体管分离组件为基础发展起来的数控系统取代了以笨重的电子管为组件搭建的数控系统，这使得数控系统的体积得到缩小，促使其在工业生成中的广泛应用，这就是第 2 代数控系统。 1965 年发展起来一种功耗低，体积更小的集成电路构成的 NC 系统，该型 NC
系统的可靠性更高，数控系统进入第 3 代。
软件数控阶段是以 1970 年小型计算机的应用为标志。同时，数控系统的发展进入到第 4 代，软件慢慢取代硬件来完成更多的功能，“软连接”数控时代开始引领数控加工的行业发展。
1974 年采用微处理器芯片的 CNC 系统开始投入使用，数控系统进入了以微机为背景的时代，同时数控系统进入到第 5 代阶段。微处理器型的 CNC 系统实现了机电一体化，这大大降低了制造成本，缩小数控系统的体积，提高了数控系统的普及程度。
1990 年发展起来的基于个人 PC 机的数控系统是第 6 代（PC-Based）。这一代是以大容量存储器、大规模集成电路、CRT 应用为标志。第 6代数控系统具备更完善的控制功能，具有实时精度补偿、三维图形显示校验、交互式编程等软件技术。同时这一代数控系统具有了模块化、柔性化、系列化、标准化的雏形。
第 6 代数控系统已经具有了明显的优点。利用 PC 平台的优势，数控系统的技术进步以及更新升级都比较快捷。第 6 代数控系统具有较高的元器件集成度，可靠性高，性能更加优越，而且第 6 代数控系统提供了开放式的开发平台，这更有利于软硬件资源优势的发挥，拓宽了数控系统的应用领域。
1958 年由北京机床研究所和清华大学研制的第一代电子管 101 数控机床标志着我国数控机床进入第一代阶段，开启了我国数控系统研制的历史序幕[2]，我国数控系统发展历史如表 1.1 所示。
表 1.1 数控系统发展历史
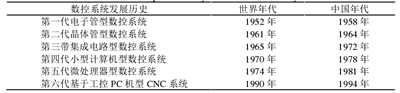
数控技术是一种将机械制造技术、成组技术、现代控制技术、计算机技术、网络通讯技术、光机电技术、微电子技术、传感检测技术、信息处理技术、液压气动技术集合在一起的系统技术，是现代制造技术的基础[3]。数控系统在数控技术中处于核心的地位，其性能的强弱直接影响数控设备加工效能的高低，而且对整个制造系统的升级发展、高效运转、自动化控制具有重要作用[4]。计算机技术的飞速发展，推动着数控系统向开放式、标准化方向发展，出现了一些不同层次的开放式数控系统[5]。新代科技股份有限公司顺应时代发展，推出了开放式的 SYNTEC 数控系统，其开放式的数控系统设计方便用户进行系统功能的二次开发。 数控是数字化控制（Numerical Control, NC）的简称。数控是指利用数字化信息实行的控制，即利用数字控制技术实现的自动控制系统[6]，这是数控的广义含义。从狭义上来说就是利用数字化信息对机床轨迹和状态进行控制，例如数控车床、数控冲床、数控铣床、数控加工中心等[7]。数控系统嵌入到机床本体中就组成了更具较高附加值的技术密集型产品-数控机床，它可以实现加工过程的自动化控制[8]
在实际的数控生产中，经常会遇到同一系列不同尺寸规格的零件，这需要每一个规格的零部件单独编制一个数控加工程序，编制程序的工作量就会很大，十分烦琐不便[9]。在西门子数控系统中，虽然自身带有某些固定循环功能可供机床操作者使用，但是它的界面不直观，不友好，且对应用场合的限制较多[10]；而在发那科系统中，虽然可通过二次开放 G 功能的方式实现固定循环，但是其界面也不够直观，不完善，对操作者的技术要求较高[11]。
1.2 弧齿锥齿轮加工现状
1.2.1 国外研究现状
英国人 Hum Phris 在 1970 年最早提出了圆弧齿形的设计思路[12]，以这个思路为基础，慢慢发展到了后来的弧齿锥齿轮。该型齿轮的齿面计算公式是非线性方程组，所以齿面形状较为复杂[13]，加工要求比较高。螺旋锥齿轮具有重合度大、传动平稳、承载能力高等直齿锥齿轮不具备的性能优点，因而这促使了该型齿轮在相交和交错轴传动场合中的广泛应用。基于该型齿轮优越的性能，对螺旋锥齿轮进行相关研究的重要性在世界范围内得到广泛的认同。而美国
Gleason 公司的 E.威尔德哈泊以及 M. L.巴斯特尔初步提出了弧齿锥齿轮理论[14]，以此为基础，Gleason 公司通过对弧齿锥齿轮的深入研究，形成了特有的弧齿锥齿轮相关技术，奠定了其在世界上的垄断地位。图 1.1是弧齿锥齿轮啮合传动示意图。
图 1.1 弧齿锥齿轮啮合传动示意图
曲齿锥齿轮分为延伸外摆线（Oerlikon 和 klingelnberg）和准双曲面（Gleason）两种齿制[15]，曲齿锥齿轮的加工制造技术要求比较高，目前世界上只有三家公司具有相关的技术，分别是美国 Gleason（格里森）、瑞士 Oerlikon（奥利康）和德国 Klingelnberg（克林根贝尔格）[16]。准双曲面齿轮在轴线相交时即为弧齿锥齿轮，其应用最广泛，这种齿轮采用间歇分齿法铣齿加工而成，调整加工的过程复杂。
国内外学者对曲齿锥齿轮进行了深入的研究。60 年代初 Gleason 公司的 Baxter 和Wildhaber 通过对局部共轭齿面副的齿面接触过程分析，提出了准双曲面锥齿轮节面数学模型理论，这提高了Gleason 公司弧齿锥齿轮理论的成熟度[17,18]。由于格里森公司在弧齿锥齿轮技术上的进步，以局部共轭原理作为弧齿锥齿轮设计和加工的基础，形成了一系列格里森制锥齿轮的设计和加工方法，巩固了其在弧齿锥齿轮加工领域的垄断地位。由于弧齿锥齿轮的加工过程是一个反复调整机床参数，反复试切的过程，加工效率比较低， Baxter 提出了弧齿锥齿轮的齿面接触分析（Tooth Contact Analysis，简称 TCA）方法。这种方法是基于计算机平台运行的，以加工机床的调整参数为依据，建立啮合齿轮的齿面数学方程，利用数学理论研究齿轮在不同安装形式下的齿面接触情况和传动误差，通过研究齿面接触区，对机床调整参数进行修正。美国的著名教授 Litvin 提出“局部综合法”[19-24]的切齿加工方法，首先给出决定齿轮啮合区宽度和位置、接触轨迹方向等传动质量的相关条件，然后利用微分几何的数学理论，推算小轮齿面在参考点处的主方向和主曲率，进而得到小轮加工的机床调整参数。Litvin 教授提出的预置抛物线型误差传递函数是这种方法的基础[25]，由于安装误差所造成的线性传递误差可以通过这种方法自动吸收掉，这对于齿轮传动中振动、冲击以及噪声的降低是有利的。
（1）Gleason 公司锥齿轮加工系统准双曲面锥齿轮加工机床是美国 Gleason 公司的主要经营产品，是格里森公司具有自主知识产权的机床，但是它采用的是齿轮传动机构，其机械传动机构比较复杂[26]，由传动链较长引起的制造误差比较明显。二十世纪八十年代，格里森公司以凤凰系列螺旋锥齿轮加工机床为标志，掀起了该类机床的重大改革创新。这种机床是一种五轴联动的多功能机床，可加工多种齿制的螺旋锥齿轮，除了需要手动更换夹具、刀盘、工件以外，其余的加工过程均是自动化完成的，相对机床来说，加工精度能够高出 1-2级，而且重复精度较好。格里森公司与德国 Zeiss 公司合作开发了误差分析和三座标测量系统，将这个系统连接到凤凰系列机床上，构成误差闭环系统：G-AGE。该系统在准双曲面加工中可以通过一次试切的方式获得满意的啮合配对。
在 CIMT-99 展会上，SRS405 型数控剃齿刀磨床和 450G 型数控螺旋锥齿轮磨齿机被格里森公司以凤凰系列主力机型的形式推出了。450G 型磨齿机可以按照 3-4 级精度精磨啮合的硬齿面螺旋锥齿轮小轮和大轮，其加工工件的最大模数为 12mm，最大加工直径达到了 450mm，联轴节齿面或者弧齿鼠牙盘也囊括在其加工范围之内，表现出了优异的加工性能。450G 型数控机床可以实现包括砂轮修整运动在内的八轴联动，它用其中的五轴联动实现了锥齿轮加工中的磨齿运动[27]。目前格里森公司生产的较为成熟的数控磨齿机有 200G、450G、800G 以及铣齿机 Phoenix116CNC、175HC、275HC、450HC、100HC 等系列产品。
（2） Oerlikon 公司锥齿轮加工系统 瑞士 Oerlikon（奥立康）公司在 CIMT-99 展会上展出了一台可实现干切削的型号为 C28 的六轴五联动的数控螺旋锥齿轮铣齿机[27]。为了排屑的方便，该型机床将刀盘主轴箱的滑鞍安装在了倾斜床身的导轨上。我国湖北省某车桥有限公司曾于 1997 年引进了 Oerlikon 公司的 C28 型铣齿机，该车桥公司成为中国第一家采用该型数控铣齿机的用户。随着生成的发展，这种环保型数控铣齿机以其优异的加工性能受到各企业的青睐，慢慢发展成为汽车后桥主从动螺旋锥齿轮加工的关键设备。
（3）Klingelnberg 公司锥齿轮加工系统 Klingelnberg（克林根贝尔格）公司开发出一种型号为 KNC/S35 的万能数控弧齿锥齿轮切齿机床，该型机床把齿轮测量技术内嵌到机床中，精简了机床机构，改善了机床的刚性；提高了机械的响应速度，保证了 NC 指令的可靠性，齿轮加工的精度得到提高。将计算机技术应用于齿轮加工机床可以提高加工精度，降低生产成本，增大负载能力和降低噪声。Klingelnberg 公司采用新的计算机技术之后推出 HPG、HPG-S 两种型号的锥齿轮加工机床。
1.2.2 国内研究现状
为了打破格里森公司在弧齿锥齿轮加工领域的技术壁垒，前苏联和日本等国的科学家对格里森制齿轮进行了研究和学习，相关的研究学习虽然推动了弧齿锥齿轮理论的发展，但是始终没有突破弧齿锥齿轮的啮合理论问题。我国的相关技术人员从 70 年代开始对弧齿锥齿轮啮合理论的数学基础进行了系统的研究。为了推进该技术的研究进展，我国原机械工业部于 1972 年将“格里森成套技术的研究”列为重点攻关的科研项目，同时得到了许多知名学者、高等院校的支持。我国科研人员通过不懈的努力，在弧齿锥齿轮啮合理论方面取得了重大进展[28]。龚道香教授等相关学者通过研究计算，得到了螺旋锥齿轮的齿形精密测量以及相应的误差处理方法[29]，为了求得实际齿面和理论齿面之间的偏差函数，先用误差补偿的方法求得齿形误差，再用该齿形误差作为全齿面比较法的初始值来求解。郑昌启教授利用严谨的数学解析法对共轭齿轮啮合理论中的基本原理进行了研究[30,31]，以此为依据，推算揭示了 Gleason 螺旋锥齿轮的机床调整、齿坯设计、刀具参数的计算和轮齿检验原理以及方法。曾韬教授提出了节面分析法[32]，利用该方法对准双曲面齿轮的节点曲率和节点参数进行计算，将相关的计算结果推送给螺旋锥齿轮的切齿计算和轮坯设计，推算出格里森调整计算卡的相关公式。
李左章、王延忠等教授学者采用三次 B 样条函数的数学理论对齿面采样数据点进行数值拟合[33]，由此得到齿面的拟合函数，归纳出了基于齿面离散数值点的接触分析理论。苏智剑教授利用齿面接触迹线、齿面 NURBS、传动比函数等已知条件对准双曲面齿轮齿面的数学模型进行了描述[34,35]，丰富了螺旋锥齿轮的设计计算方法和理论。
1.3 课题研究的目的与意义
以我单位引进的新代 SYNTEC 数控系统为平台，针对弧齿锥齿轮的数控加工过程，对其进行二次开发，通过编程，将现有的先进控制思想应用到数控系统中，完善其控制算法，优化数控加工的参数输入界面、模拟仿真界面，使其能够通过屏幕界面直接输入弧齿锥齿轮的一些基本参数，生成相应的数控加工程序，然后进行自动化加工。 数控系统是衡量一个国家制造业发展水平的重要指标，在制造业中处于核心的位置。作为我国国民经济的核心以及工业化的原动力，制造业的总产值大约占全国国民生产总值的百分之四十左右。虽然制造业是我国国民经济的支柱产业，但是数控技术的发展水平较国外发达国家相比差距较大，这限制了我国制造业的发展[36]。
装备制造业在世界范围内蓬勃发展，信息技术在装备制造业相关技术产品的升级换代中表现出的积极作用越来越得到大家的重视与认可。数控技术与控制技术、计算机技术、应用软件相结合，推动了数控系统的开发，树立了传统制造业信息化改造的典范。而先进控制技术的主要任务是使数控机床具有最大化的加工速度、加工速度平滑性以及较小的加工误差，通过与先进的制造技术结合，缩小了国内与国外在硬件技术和软件技术上的差距，这对于完善我单位项目中引进的新代 SYNTEC 数控系统的功能，总结数控系统开发过程中的经验，提升国产数控系统性能和品质具有重要意义。
研究采用计算机仿真、优化的虚拟加工技术，实现了从加工编程到加工仿真的全程虚拟化，可以有效的缩短产品生产周期，减小生产成本。基于新代 SYNTEC-10B 数控系统平台的弧齿螺旋锥齿轮加工机床人机界面设计，能够提高锥齿轮加工的人机交互性，提高齿轮的加工效率。新代数控系统人机界面的客制能够适应螺旋锥齿轮系列化生产中由于生产批次与型号的变更，对数控编程提出的便捷性要求。因此，本课题的研究内容对加快产品研发，缩短制造周期，促进螺旋锥齿轮的应用范围以及整个机械行业的发展都有着很高的现实意义。
1.4 课题研究内容
台湾新代科技股份有限公司顺应行业发展的需要，推出了便于用户二次开发的SYNTEC 系列的数控系统，它是一个良好的开放式平台，通过二次开发可把客户需要的各功能模块集成到系统中，这样既可以将操作者工作经验的优势发挥出来，又可以简化工作流程，提高系统的可维护性。 本课题以新代 SYNTEC 数控系统为开发平台，以螺旋锥齿轮加工机床为研究对象，针对弧齿锥齿轮的加工进行了数控系统的二次开发。通过 e HMI 软件对螺旋锥齿轮加工过程中参数输入、模拟仿真等相关界面进行设计与客制。设计开发的界面系统主要包括齿轮参数输入、刀具参数设置以及加工参数设置等内容，客制的人机界面简洁友好，便于操作。通过整个分析设计过程，最终达到界面参数的输入、加工代码的生成、加工仿真程序运行整个过程的虚拟化和快速化，初步总结数控加工中参数的优化和加工仿真过程的一般方法。图 1.2 是 e HMI 的软件工作界面，图 1.3 是螺旋锥齿轮加工机床样机，图 1.4 是弧齿锥齿轮数控铣齿机示意图。
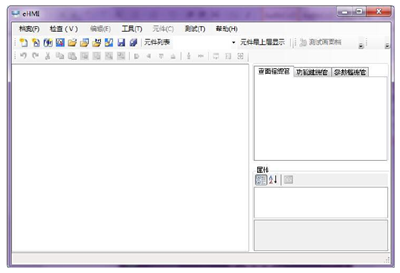
图 1.2 e HMI 工作界面
图 1.3 螺旋锥齿轮加工机床样机
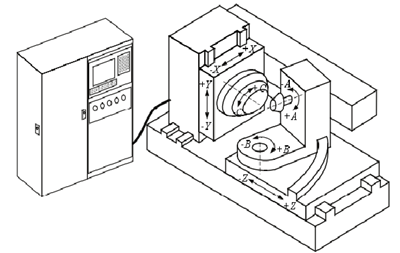
图 1.4 弧齿锥齿轮数控铣齿机示意图
1.5 本章小结
本章对课题来源及背景进行了阐述，通过对 Gleason 公司锥齿轮加工系统、Oerlikon公司锥齿轮加工系统以及 Klingelnberg 公司锥齿轮加工系统的分析，引出了对项目中的新代数控系统进行客制化改造的必要性，提出了课题研究的目的意义以及课题研究的主要内容。
第 2 章 弧齿锥齿轮加工原理
弧齿锥齿轮的数控加工过程涉及到的参数比较多，各参数之间的关联性比较大，导致相关计算过程比较繁琐；为了配合 SYNTEC-10B 数控系统的人机界面开发的项目需要，对弧齿锥齿轮的啮合加工原理作简单分析。
2.1 弧齿锥齿轮啮合原理
弧齿锥齿轮啮合原理以啮合中运动曲面接触传动关系为主要研究内容，如图 2.1所示。局部共轭理论以及相对微分法是研究啮合原理的主要方法理论，首先以啮合方程为起点，然后通过相对微分的数学理论，以节点为计算参考点，确定完全共轭时瞬时啮合点处的挠率和曲率，最后推算计算参考点处的曲面参数[14]。
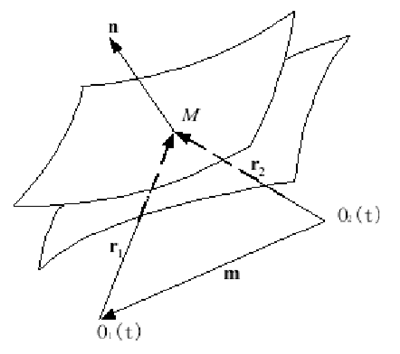
图 2.1 运动曲面的接触传动
2.1.1 相对微分法
通过上述分析得知：相对微分法能够兼顾运动中曲面的几何问题以及运动问题，是研究齿轮啮合问题的有效工具。
2.1.2 啮合方程
式子中的第一个方程是接触条件方程，第二个方程是相切条件方程。这是齿轮传动的基本方程式。
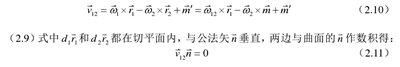
式（2.11）即为啮合方程，它表示两运动曲面持续啮合的前提条件是两曲面在法线方向的分速度必须相等。
如果两运动曲面在任何时刻都沿着啮合方程所确定的曲线接触，则称它们为线接触共轭曲面，即完全共扼曲面；如果两运动曲面在任何时刻的接触状态是在线上，则称它们为点接触共轭曲面，即不完全共轭曲面[37]。这两种啮合形式在啮合位置处都满足啮合的基本方程（2.8）和（2.11）。
2.1.3 确定第二共轭曲面
在齿轮啮合原理中经常会遇到求解某一共轭曲面的问题，即根据一对共扼曲面中的第一共轭曲面s1和两个曲面之间的相对运动关系，求解第二共轭曲面s2 。如果两个曲面能够正常啮合，那么曲面S 2必定是啮合方程所确定的接触线在运动坐标系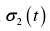 
中的轨迹，所以曲面S2满足方程组[37]：
中的轨迹，所以曲面S2满足方程组[37]：
2.1.4 等距共轭曲面原理
（1）等距曲面
设有两个曲面 S 和Sh，若对曲面 S 上任意一点 M，在曲面S h上都能找到一点 Mh和它相对应，曲面 S 上M点的法矢和曲面nS 上 Mh点的法矢都与MMh平行，而且MMh=h是一个常数，那么曲面S h称为曲面 S 的等距曲面[37]。如图 2.2 所示，若曲面 S 的方程为 r ，单位法矢为 n ，则曲面Sh 的方程可以表示为：
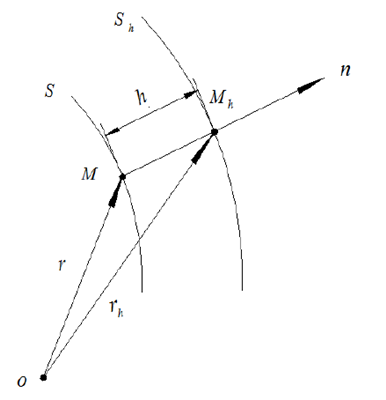
图 2.2 等距曲面样图
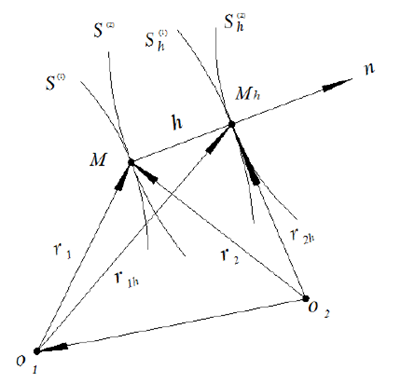
图 2.3 等距共轭曲面样图
2.2 弧齿锥齿轮加工分析
2.2.1 弧齿锥齿轮加工原理和方法
项目中的弧齿锥齿轮加工采用的是平顶产形轮原理，其中大轮是右旋，它在加工时采用的是双面铣刀盘；小轮是左旋，它在加工时采用的则是单面铣刀盘。
弧齿锥齿轮与准双曲面齿轮的加工都是在准双曲面铣齿机上完成的。该型机床的设计加工原理如图 2.4 所示，机床的摇台机构模拟齿轮，而安装在摇台上的刀盘的切削面则是模拟齿轮的一个轮齿。当被加工齿轮轮坯与刀盘按照规定的传动比绕各自的轴线旋转时，刀盘就会在轮坯上切出一个齿槽。整个切削过程就像一对准双曲面齿轮的啮合过程一样，刀盘的切削面与轮坯的轮齿曲面是一对完全共轭的齿面，称这种加工方法为展成法[37]。
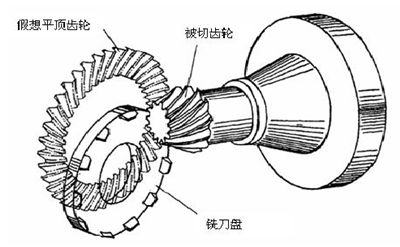
图 2.4 螺旋锥齿轮加工原理图
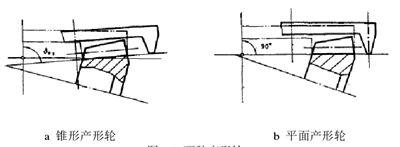
图 2.5 两种产形轮
为了能够在弧齿锥齿轮的齿面展成加工中完成齿根曲面的加工，应该保证工件的根锥与刀盘的刀尖平面相切。图 2.6 是大小轮啮合时的刀盘位置图，通过图 2.6 可以发现刀盘轴线不平行，这决定了实际加工时既不能像用展成法加工大轮一样将小轮加工用的刀盘切削面做得和小轮切削面一样，也不能使大轮刀盘切削面和小轮刀盘切削面相互吻合，而用间接展成法完成加工。所以弧齿锥齿轮不能通过间接展成法和直接展成法完成加工，需要局部共轭原理来加工[37]。
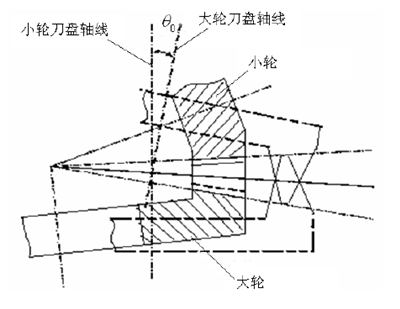
图 2.6 齿轮啮合时刀盘的相对位置
2.2.2 局部共轭原理
根据成形法或展成法加工完成的大轮齿面，结合齿轮啮合原理，求出与大轮共轭的相应小轮的齿面。求出的小轮齿面不能在铣齿机上完成加工，为了得到一个与理想齿面相切并且可以被铣齿机加工出来的实际齿面，需要将小轮齿面上选择的某点 M 四周的齿面刮去一层，如图 2.7 所示，完成对理论齿面的修正。这样处理之后，与大轮齿面相啮合的实际接触区就会是一个以 M 点为中心的局部接触区，这就是齿轮啮合的局部共轭原理[30]。
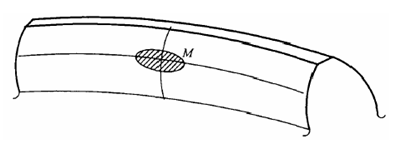
图 2.7 局部接触区示意图
完全共轭的齿轮副具有承载能力大、噪声低、运动平稳等优点，但是该型齿轮副也存在可调性差的缺点，对相关零件制造、安装误差的要求较高，如果制造安装的过程中出现的误差较大，轮齿边缘就会在啮合传动过程中出现载荷集中而使破坏的问题。局部共轭的齿轮副能够克服该缺点，即使在安装位置存在误差的情况下，也能够保证接触区只能在中点附近移动，避免载荷在轮齿边缘集中[37]
。基于局部共轭齿轮副在实际生成应用中的优良性能，准双曲面齿轮以及其他可以用直接、间接展成法加工的齿轮副，越来越多地开始采用该方法加工。
2.3 弧齿锥齿轮齿面建模
2.3.1 坐标系及参数
（1）工件位置基本参数
1）垂直轮位E02垂直轮位是指被切齿轮的中心线与摇台中心线的相对垂直偏置量。
2）床位BX2 工件箱沿摇台中心线方向相对于标准位置前进或后退的距离即为床位。它对被切齿轮的切齿深度具有直接影响。
3）轴向轮位修正值X2 工件箱在转动底座的水平轨道上移动的距离就是轴向轮位修正值X2，它用来调整齿轮在机床上的轴向位置。
（2）刀具位置基本参数
1）径向刀位S2
刀盘中心02O 到大轮加工坐标系原点 O 的距离即为径向刀位S2。
2）参考点 M 的相位角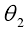
参考点 M 点相位角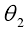
是用来表示参考点在坐标系中角相位置的参数。该参数可以完成刀盘在齿长方向的切削加工运动的控制。
是用来表示参考点在坐标系中角相位置的参数。该参数可以完成刀盘在齿长方向的切削加工运动的控制。 3）角向刀位q2 刀盘中心O02和大轮加工坐标系原点 O 的连线与 i 轴的夹角即为角向刀位q2 。刀盘在齿高方向的切削加工运动就是由该参数控制完成的。除了工件位置参数以及刀具位置参数之外，还有大轮与产形轮的传动比，即滚比02i参数，这也是弧齿锥齿轮齿面模型建立的重要参数。
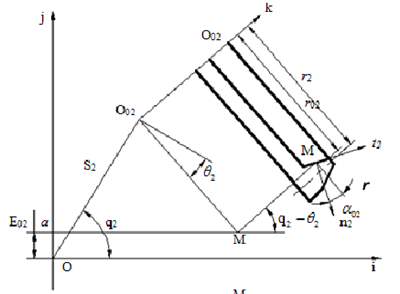
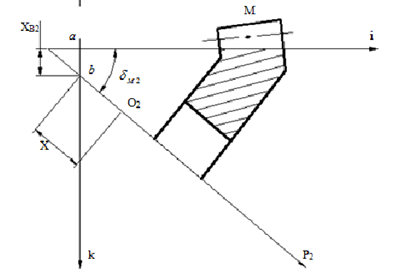
图2.8 大轮加工坐标系
2.3.2 弧齿锥齿轮齿面方程
以螺旋锥齿轮右旋大轮为例，论述齿面方程的建立过程。图 2.9 为展成法加工螺旋锥齿轮大轮时所用的双面刀盘的轴截面，图中a1为双刀面内刀面齿形角，a1 为双刀面外刀面齿形角，r0为大轮刀盘的名义半径，W2为刀刃的刀顶距。通过式子（2.22）推算加工大轮凸面的内刀和加工大轮凹面的外刀的刀尖直径[14]。
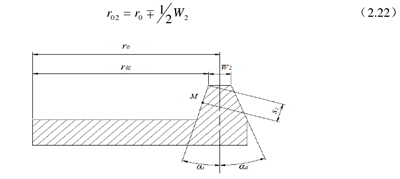
图 2.9大轮加工用双面刀盘
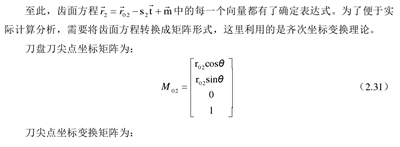
大轮齿面与刀盘切削面是共轭的，可以通过共轭曲面的方法求得大轮的齿面方程。
假设切削面为第一曲面，大轮为第二曲面，采用第二共轭曲面的求解方法建立大轮的齿面方程。
2.4 本章小结
本章主要对螺旋锥齿轮加工理论的相关知识进行了介绍。阐述了啮合原理，分析了能够解决齿面几何问题和运动问题的相对微分法，通过啮合方程的建立得出运动曲面持续啮合的前提条件是两曲面在法线方向的分速度必须相等。对弧齿锥齿轮的加工原理和方法进行了研究，分析了齿轮啮合的局部共轭原理以及弧齿锥齿轮齿面建模的过程。相关啮合理论是数控系统后台计算处理工作的主要依据，为后续章节人机界面的开发设计提供了理论支撑。
投稿箱：
如果您有机床行业、企业相关新闻稿件发表，或进行资讯合作，欢迎联系本网编辑部， 邮箱：skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表，或进行资讯合作，欢迎联系本网编辑部， 邮箱：skjcsc@vip.sina.com
名企推荐
专题点击前十
| 更多
