高速电主轴滚珠轴承-转子系统 动态性能分析
2016-8-15 来源:哈尔滨工业大学 作者:张阿祺
在高转速运转下,由于球滚动体绕自身轴线会转动并且绕轴承轴线也有转动,这时球滚动体不是简单的单一运动,而是产生滚动和滑动结合的复合运动,球滚动体的陀螺力矩、摩擦力和相应的离心力值通常会很大,摩擦力会受到较大的影响,使得外滚道发生了比较大的变形,使球滚动体的内部载荷分布发生变化。高速角接触球轴承动力学求解的关键是内外圈与滚动体的接触角,所有的动力分析都跟接触角有关,所有求解的关键也必然是接触角。
3.1 高速状态下的滚动体运动状态分析
3.1.1 轴承中的坐标系
如图 3-1 所示,以角接触球轴承绕 x 轴高速旋转的某个球滚动体为质点,建立了三个坐标系:
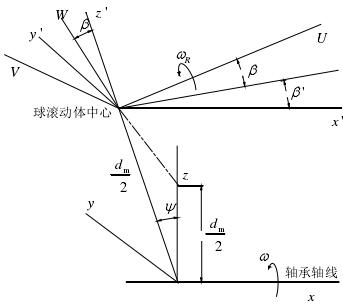
图 3-1 轴承各坐标轴及其关系
(1)x,y,z 轴承固定坐标系,x 轴的方向与轴承旋转轴的方向一致;
(2)x’,y’,z’滚珠随动坐标系,x’轴与 x 轴平行,原点 O’为滚珠球心且绕x 轴以轨道速度旋转,旋转半径为md/ 2 ;
(3) U,V,W 以 O’为原点并以轨道速度绕 x 轴旋转,以滚珠自身旋转轴为 U 轴, W 轴位于 U 轴与 z’的平面内,W 与 z’的夹角为 β。
根据内圈沟道理论,轴承外圈相对固定,内圈以角速度为做匀速运动时,轴承转速为:
3.1.2 忽略陀螺枢轴运动滚动体的自转和公转运动
球滚动体的自转运动,高速状态下,主轴轴承滚动体绕自身轴线 O’U 作自转运动:
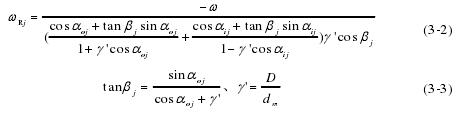

球滚动体的公转运动,主轴轴承内部球滚动体绕轴承中心线 OX 轴作公转运动时,其角速度等于保持架的角速度,大小为:
3.1.3 忽略陀螺枢轴运动滚动体的自旋运动及旋滚比
滚珠的自旋运动(非控制沟道即内圈沟道存在自旋运动),本文是以外圈沟道为控制沟道的高速电主轴轴承,跟其他理论体系认为存在复合运动的情况不一样,外圈沟道控制理论认为外圈滚道只作纯滚动,并不存在自旋运动,从而简化了研究对象,内圈沟道既作滚动运动又绕接触面法线做自旋运动:
内圈沟道的旋滚比为:
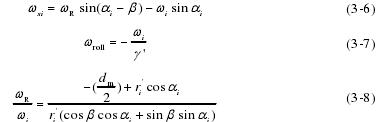
由式(3-6)、(3-7)、(3-38)得内圈沟道的旋滚比为:
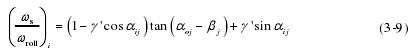
3.2 高速状态下滚动体的受力状态分析
3.2.1 离心力
高速运转状态下的轴承内部滚动体会受到比较大的离心力作用:


3.2.2 陀螺力矩和摩擦力
由于主轴轴承运转时,其内部球滚动体会发生自转,使得轴承的自身轴线 O’U会不断地改变方向,并产生陀螺运动趋势,陀螺力矩将被球轴承滚道上的摩擦力所阻止。陀螺力矩可表示为:

根据外圈沟道控制理论和力平衡条件,外圈的滑动摩擦力应与陀螺力矩平衡:
3.3 轴承内部的变形和位移
3.3.1 预载荷引起轴承滚珠的变形和位移
一般轴承会施加一定的预载荷来提高轴承抵消外力载荷的能力,保证轴承系统的支承动态稳定性,即提高轴承的动刚度,从而提升轴承的性能。但是预紧载荷不能过大,因为过量的预载荷会引起摩擦力矩的增加导致轴承发热过大而影响轴承的使用寿命。轴向预载荷与轴承工作角的关系:
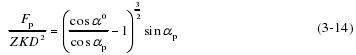

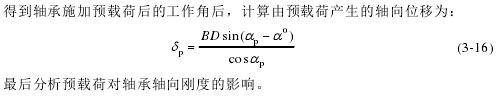
3.3.2 高速状态下轴承的内部变形和位移
由于球滚动体绕自身轴线和轴承轴线都在做旋转运动,所以会产生惯性载荷和离心力[5]。在低速状态下这些惯性载荷比外载荷小得多,可以忽略不计,但是在高速状态下,轴承内圈圈滚道曲率中心的初始位移为:
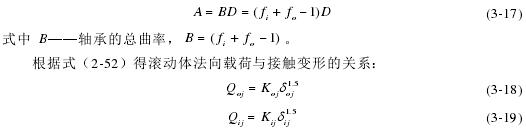
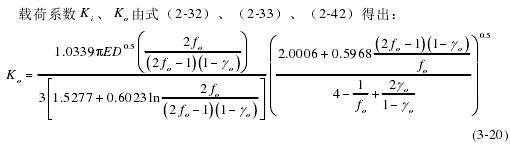
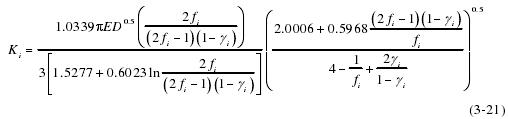
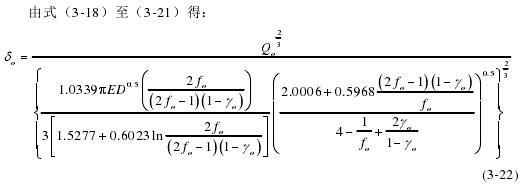
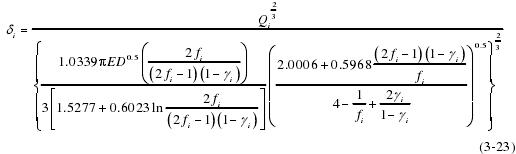
根据内、外圈的相对轴向位移、相对径向位移和相对角位移可以求出内、外圈沟道曲率中心轨迹的轴向距离和径向距离分别为:
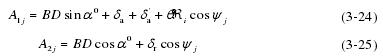
由图 3-2 可以得出各个参数之间的关系:
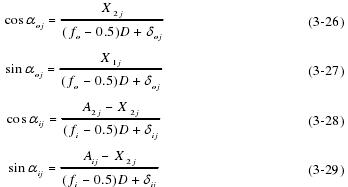
根据勾股定理和相应滚道接触变形的几何协调条件:
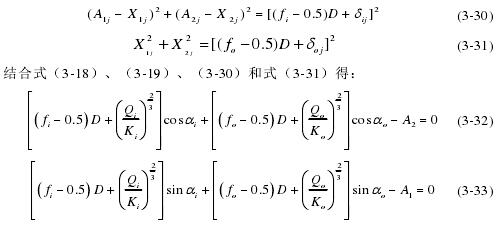
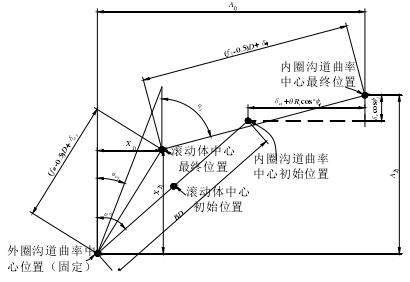
图 3-2 载荷作用前后角位置Φ 处球中心和沟道曲率中心的位置关系
3.4 高速状态下轴承的受力方程和基本方程组
3.4.1 球滚动体受力的平衡方程组
根据高速电主轴运行的实际情况,外沟道控制基本成立,滚动体的陀螺力矩完全被球-外沟道接触区的摩擦力所阻止。滚动体所受载荷的关系如图 3-3 所示,那么可得到水平和垂直方向的轴承内部受力平衡方程组:
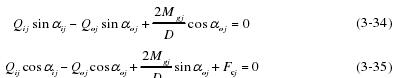
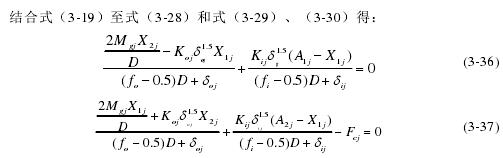
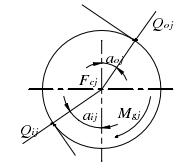
图 3-3 角位置Ψ处球滚动体所受载荷
3.4.2 轴承受力的平衡方程组
轴承在轴向、径向和绕轴线转动方向受力平衡,则整个轴承的平衡条件:
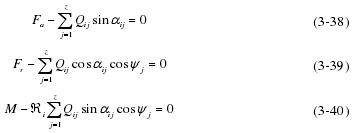

3.5 轴承方程组的求解和动力学状态分析
3.5.1 轴承方程组的求解优化及其流程图

由式(3-27)、(3-29)得:
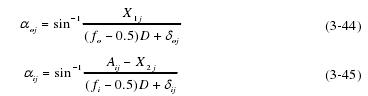
很多文献包括 Harris,都是应用 Newton-raphson 迭代法进行求解 4Z+1 个方程组,这个方法用于求解低数量方程组成的方程组效率挺高的,但是求解多个方程组成的方程组会出现很大的问题,甚至无法收敛。Newton 法存在的缺陷主要有:
(1)需求解 N2个导数值;
(2)对初值要求很高;
(3)需对 Jacobi 矩阵求逆,而此非线性方程组的 Jacobi 矩阵可能是病态的。
通过此法求解轴承非线性方程,很容易造成不收敛或者求解时间过长,并且初值是由静态值求得的,精度很低,很难满足 Newton 法的要求。


采用逆 Broyden 秩 1 法的主要优点有:
(1)只需求解 N2个算数运算;
(2)无需求解 Jacobi 矩阵的逆。
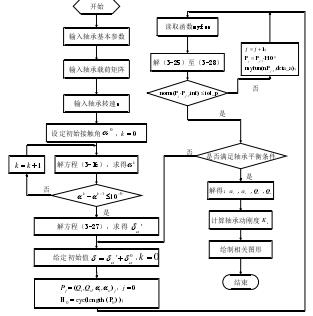
图 3-6 高速球轴承动力学状态分析程序流程图
(2)通过优化求解方程组,最后高速球轴承动力学状态分析流程如图 3-6 所示,利用此程序流程图编写 MATLAB 程序,求解轴承方程组,并得到如表 3-1 所示数据。当 n=10000 r/min,Fa=20000 N,Fr=0 N 时,本文结果通过和 Harris结果对比基本一致,Harris 结果是在一定的实验基础上得到的,说明所编制程序求得的结果在误差范围内符合实际结果。
表 3-1 球轴承 7218 内部动力学状态对比

3.5.2 预载荷对轴承初始量的影响
对轴承施加预载荷在一定程度上能使轴承的刚度增加,减少噪音并提高轴承的工作精度,但是预载荷过大则降低轴承的使用寿命,过小则得不到预期的效果。
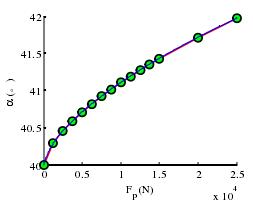
图 3-4 预载荷与实际接触角的关系
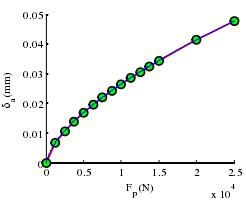
图 3-5 预载荷与轴承初始位移的关系
(1)预载荷对轴承实际接触角的影响如图 3-4,当增大预载荷时,轴承的实际接触角随之变大,但是增加的趋势变小,即斜率变小,所以在施加预载荷时应控制其大小,以免轴承的工作接触角过大,使得摩擦力增加,进而影响轴承寿命。
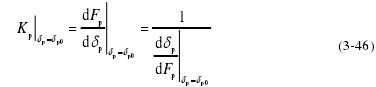
(2)预载荷对轴承初始位移的影响如图 3-5,当增大预载荷时,轴承初始位移也随之增大,但是趋势在一定程度上减小。由式(3-46)结合图 3-5 可以得出,命产生影响。
3.5.3 转速对轴承动态性能的影响
轴承转速对轴承动态性能有很大的影响,它是衡量轴承性能的重要参数。轴承转速越高,主轴机床的加工性能越好,但是轴承转速越高,其对轴承内部动力学特性影响越大。转速 n 引起了轴承滚动体的离心力和陀螺力矩的变化,也改变了轴承滚动体在滚道上的实际接触角,实际的滚道接触载荷等轴承内部动力学量。
(1)转速对轴承滚道实际接触角的影响如图 3-7,主轴轴承在高速状态时,由于滚动体的离心力和陀螺力矩的影响,滚动体会远离内圈趋向外圈,使得内圈接触角增大而外圈接触角减小。转速越高,滚动体的内外圈实际接触角的值相差越大。
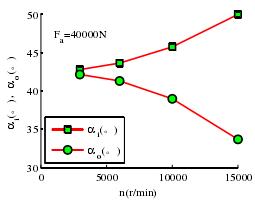
图 3-7 转速与滚道接触角的关系
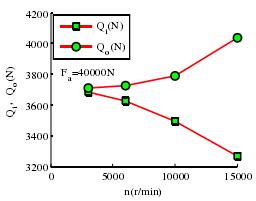
图 3-8 转速与滚道接触载荷的关系
(2)转速对轴承接触载荷和接触应力的影响如图 3-8 和图 3-9,主轴轴承在高速运转时,其滚动体在内圈接触载荷和接触应力在减小,减小幅度较小;在外圈滚道上接触载荷和接触应力在增大,在转速超过 10000r/min 时变化幅度很大。在转速超过 15000r/min 时内外圈的接触载荷和接触相差很大,对轴承性能产生很大的影响。
(3)如图 3-10 转速对轴承接触位移的影响,转速提高时,轴承的轴向位移减小,而且减小趋势变快,由于 Fa不变,轴向位移减小,所以此时轴承的轴向刚度稍微变大,对轴承性能产生有益的一面。但是这个影响有限,需要我们权衡利弊。
(4)转速对离心力、陀螺力矩的影响如图 3-11 和图 3-12 所示,高速状态球轴承随着转速的提高,轴承球滚动离心力体会随之增加达到了相当大的值,陀螺力矩也是一样的。离心力是球滚动体的惯性特性引起的,这时已经成为影响轴承内部动力学状态的主要因素,而由于陀螺力矩是由外圈摩擦力来抵消的,其值过大将使外圈摩擦力增大,发热变大,进而影响轴承动态性能。
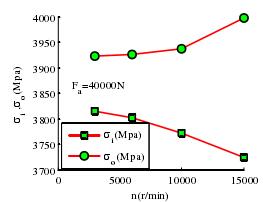
图 3-9 转速与内外圈最大接触应力的关系
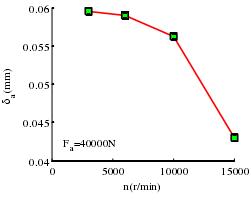
图 3-10 转速与轴向位移的关系
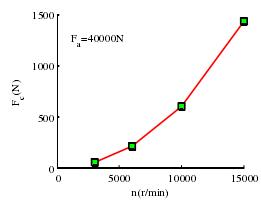
图 3-11 转速与离心力的关系
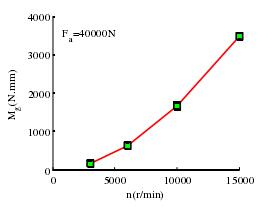
图 3-12 转速与陀螺力矩的关系
(5)从图 3-13 可以看出转速对旋滚比的影响,随着转速的提高,轴承滚动体在内圈的旋滚比迅速增加,使得球与内圈滚道的滑动摩擦增加进而发热加剧,严重影响轴承的正常工作降低轴承的疲劳寿命。
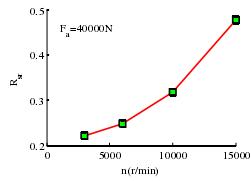
图 3-13 转速与内圈旋滚比的关系
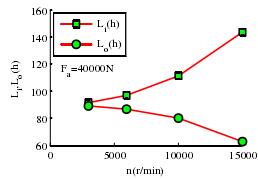
图 3-14 转速与轴承内外圈疲劳寿命的关系
(6)转速对轴承内外圈的疲劳寿命的影响如图 3-14,随着转速的提高,内圈疲劳寿命不断增加,而外圈的疲劳寿命却剧烈降低,这是因为转速增加后内圈的接触载荷和接触应力在减小,而外圈却大幅增加的关系。
3.5.4 不同转速下的推力作用载荷对轴承动态性能的影响
本文设计主要针对高速主轴所受轴向力影响,径向载荷和倾覆载荷都比较小,可以忽略。同时轴承处于稳定工作环境下,轴向载荷受的冲击很小很平稳。
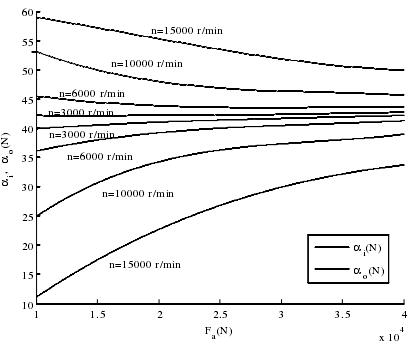
图 3-15 推力作用载荷与接触角的关系
(1)推力作用载荷对滚道实际接触角的影响如图 3-15,当推力作用载荷变大时,轴承的内圈接触角减小,外圈接触角变大。低速时推力作用载荷对接触角的影响较小,高速时接触角变化率很大,接触角趋向接近初始接触角,对轴承性能有一定的影响。
(2)推力作用载荷对滚道接触载荷的影响如图 3-16,随着推力作用载荷的增加,轴承内外圈接触载荷会随之增加,对轴承的运转和寿命产生不利的影响。其中在转速为 15000 r/min 时外圈接触载荷在低速时受推力作用载荷影响不大,因为这时主要受高速转速的影响。而在较低速和高速内圈的接触载荷受推力作用载荷的影响较大而且基本上成正比例关系。
(3)推力作用载荷对内外圈接触应力的影响如图 3-17,随着载荷的增加,轴承内外圈滚道接触应力随之增加,这跟推力作用载荷影响内外圈接触载荷的情形基本相同,这里不再重复叙述。接触应力的大小会影响轴承的疲劳寿命。
(4)推力作用载荷对轴向位移的影响如图 3-18 所示,随着轴承推力作用载荷的增加,轴承的轴向位移也在不断的增加,但是增加的趋势在明显的减小。由公式(3-41)可知。轴承的刚度也在随着增加,其中当转速等于 15000 r/min 时,轴承的刚度增加得最快。而在低速时轴承的刚度基本不变。
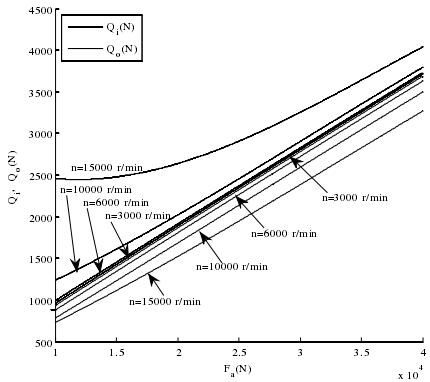
图 3-16 推力作用载荷与滚道接触载荷的关系
(5)推力作用载荷对离心力的影响如图 3-19,在低速时轴承滚动体的离心力基本不受推力作用载荷的影响,而在转速超过 15000 r/min 时离心力随着推力作用载荷的增大而减小,这是因为推力作用载荷影响了工作接触角进而影响滚珠公转转速的关系。
(6)推力作用载荷对陀螺力矩的影响如图 3-20 所示,在低速时轴承滚动体的陀螺力矩基本不受推力作用载荷的影响,而在转速超过 15000 r/min 时陀螺力矩随着推力作用载荷的增大而增大,这是因为推力作用载荷影响了工作接触角进而影响滚珠公转和自转转速的关系。由于陀螺力矩是由外圈摩擦力抵消的,其值不能超过外圈动摩擦力,不然假设不成立。
(7)推力作用载荷对旋滚比的影响如图 3-21 所示,随着推力作用载荷的提高,轴承滚动体在内圈的旋滚比有所降低,球与内圈滚道的滑动摩擦减少。此外,在低转速时推力作用载荷对旋滚比基本没有影响。
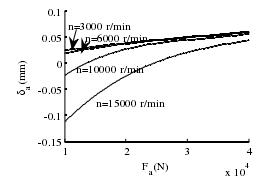
图 3-18 推力作用载荷与轴向位移的关系
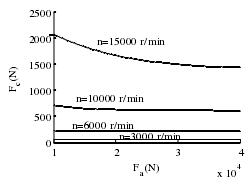
图 3-19 推力作用载荷与离心力的关系
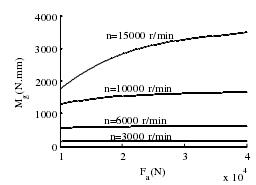
图 3-20 推力作用载荷与陀螺力矩的关系
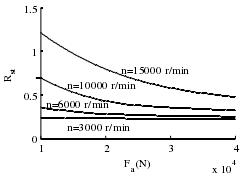
图 3-21 推力作用载荷与旋滚比的关系
3.6 本章小结
本章通过对高速角接触球轴承的分析得出以下结论:
(1)同样大小的高转速运转下,一定程度的预载荷通过对轴承的位移和滚动体与内外滚道的接触角的影响,提高轴承的动刚度,有利于轴承动态性能的提升。
(2)通过转速、推力作用载荷对离心力、旋滚比和陀螺力矩等动力学量的影响分析,可以看出高转速和不同的推力作用载荷引起了轴承滚动体运动状态的巨大变化,轴承滚动体在滚道上的实际接触角和实际的滚道接触载荷也发生很大的变化,从而改变了轴承的动刚度等动力学性能。最后也会对后面电主轴轴承-转子系统的动态性能研究产生较大的影响。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
专题点击前十
| 更多










