随着科学技术水平的不断提高,人们对机械产品的性能、寿命和可靠性的要求也不断提高,对机器及仪器零件的加工精度要求愈来愈高,各种高硬度材料的使用也日益增加。此外由于精密铸造与精密锻造工艺的进步,许多零件可以不经过车削、铣削直接由毛坯磨制成成品,从而使得磨削加工获得了越来越广泛的应用和迅速发展[1]。在磨削加工中,表面完整性可以用来衡量磨削加工表面质量的好坏,目前对于零件表面完整性的要求也越来越高,它主要包含表面纹理指标与表面层物理力学性能指标两类[2]。而工件表面粗糙度是表面完整性指标中极为重要的一个参数,也是决定磨削加工质量的重要因素之一。粗糙度的大小对工件使用性能有很大的影响,表面粗糙度越小,零件的耐磨性、耐疲劳性、耐腐蚀性相应就越好,并且可提高零件装配时的配合精度。
目前国内外将智能算法运用于表面粗糙度预测的应用研究越来越多,但是其侧重点不一样。河海大学的林岗等人使用模糊自适应BP 算法建立了影响表面粗糙度参数与工件表面粗糙度之间的关系模型,依据给定的数据样本对模型进行训练,将训练好的网络进行实际的表面粗糙度预测。湖南大学的李波等人建立了基于BP 神经网络的表面粗糙度声发射预测模型,以声发射信号有效值、FFT 峰值和标准差作为网络输入,对高效深磨陶瓷工件表面粗糙度进行预测。吉林大学的李晓梅等对影响磨削表面粗糙度的12个因素进行了讨论,并选择其中7 个主要因素建立了模糊网络粗糙度预测模型。AL-AHRNARIF对BP 神经网络模型和线性回归模型进行了对比,结果显示神经网络模型比线性回归模型更有优势。NALBANT等研究了切削参数及刀具材料对车削表面粗糙度的影响,并建立了3 层BP 神经网络,对加工过程的表面粗糙度进行预测。
从以往的研究中可以看出: 人工神经网络预测模型具有良好的预测精度,并且不同于回归分析,它不需要一开始就建立输入参数和输出参数的数学模型。在以往的分析研究中,由于BP 人工神经网络具有很好的函数逼近性能、结构简单、可操作性好,故所用的模型多为BP 网络模型。但需要指出的是: BP 网络存在收敛速度慢、网络学习和记忆具有不稳定性、容易陷入局部最小值等缺点,在实际应用中,需要对BP 网络算法进行改进。文中主要利用学习速度快、泛化能力和逼近性能更强的径向基函数RBF 神经网络来对磨削表面粗糙度进行预测研究。
1 磨削表面粗糙度智能预测的基本框架
首先根据已有的经验数据集或者实验数据训练神经网络,应保证在网络训练完毕之后使其已经具备了计算磨削参数的能力。由于RBF 神经网络具有很好的函数逼近性能,通过一定数量的磨削实验数据进行网络训练,可以拟合出在一定磨削加工条件下的磨削表面粗糙度的预测模型。将对磨削表面粗糙度影响较大的磨削工艺参数作为输入参数输入网络中,通过已经建立好的RBF 神经网络预测模型得出期望输出的磨削表面粗糙度值。具体的磨削表面粗糙度智能预测的基本框架图如图1 所示。
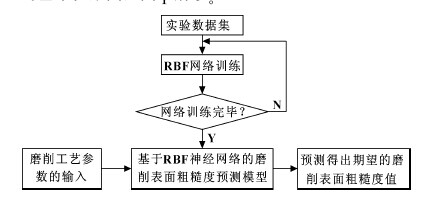
2 RBF 神经网络基本理论
2. 1 RBF 神经网络结构
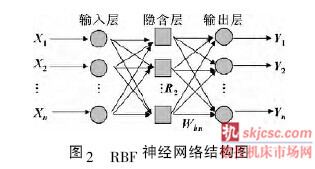
径向基函数RBF 神经网络是只有一个隐藏层的3层前馈神经网络类型,其网络结构可以表示为如图2所示。在该网络中,输入层只起到传输信号的作用,输出层和隐层的学习策略并不一样。输出层是调整线性权值,采用策略是线性优化,而隐层是对激活函数的参数进行调整,采用的策略是非线性优化。构成RBF 网络的基本思路是用RBF 作为隐含单元的基构成隐含空间,这样就可将输入矢量直接映射到隐空间[9]。与其他前向网络相比最大的不同在于: 隐层的转换函数是局部响应的高斯函数,而以前的前向网络的转换函数都是全局响应函数。正是由于局部响应的特点,它能够以任意精度逼近任意连续函数,并且具有全局逼近的特点,不存在陷入局部最小值问题,同时它具有良好的泛化能力,计算量小,学习速度也比一般其他算法要快。
2. 2 RBF 神经网络的学习算法
在RBF 网络的学习算法中,需要求解的主要参数有3 个: 基函数的中心、方差以及隐含层到输出层的权值。依据径向基函数中心选取方法的不同,RBF网络的学习方法也有所不同,如有随机选取中心法、自组织选取中心法、有监督选取中心法和正交最小二乘法等。目前用得比较广泛的是自组织选取中心法,其学习算法的具体步骤[11]如下:

3 磨削表面粗糙度预测模型的建立
3. 1 影响表面粗糙度的因素
磨削加工是一个复杂过程,受众多的输入因素影响,磨削结果通常缺乏一定的必然规律。同样,影响磨削加工表面粗糙度的因素也有很多,有工件材料的化学成分、工件的尺寸大小、金相组织、砂轮特性、修整状况、磨损程度、砂轮线速度、工件速度、磨削深度、材料去除率与磨削液等[2]。归纳起来主要受3 方面的影响,即工件材料信息、砂轮信息和加工条件信息。由于在实验过程中工件材料信息及砂轮信息一般都是给定的,所以文中主要考虑加工条件信息,即砂轮线速度、工件速度、磨削深度、材料去除率这4 个主要影响因素对工件表面粗糙度的影响。
3. 2 样本数据的获取
3. 2. 1 磨削实验条件
实验用机床。实验在MGKS1332 /H-SB-04 型高速外圆磨床( 如图3) 上进行。砂轮架部件采用闭式静压导轨形式,并采用伺服电机和精密丝杠的传动结构; 砂轮轴系采用高速滚动轴承和内装式电机结构,砂轮主轴装有SBS 动平衡仪。头架采用伺服电机和同步带传动结构,头架主轴系统为滚动轴承形式的成熟结构。床身为整体铸件,具有良好抗振性和热稳定性。

磨削试件材料为20CrMnTi,表面渗碳淬火,单边渗碳层深度为1. 5 mm,磨削外圆直径为插入80 mm,外圆轴向尺寸为18 mm。磨削砂轮为99VG3A1-400-22-5,最高砂轮线速度为150 m/s,陶瓷结合剂。测量仪器。此实验采用JB-4C 精密粗糙度仪对擦净后的磨削试件的表面粗糙度进行测试。在给定的取样长度内,在垂直于磨痕的方向上测量被加工表面的粗糙度Ra,在每种工况条件下选择3 个不同位置测量,并取其平均值。
3. 2. 2 实验工况及测量数据
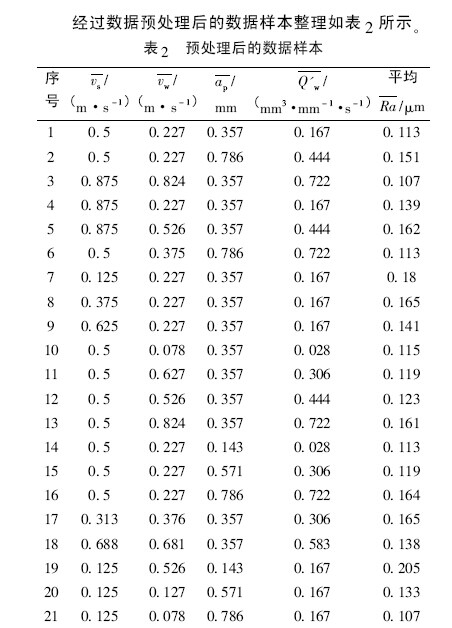
每次实验前,先要对砂轮进行动平衡,使用在线动平衡仪( SBS) 按照相应的砂轮线速度进行平衡,当平衡量达到0. 03 μm 后开始实验。实验采用乳化液冷却,切入外圆磨削。每完成5 组实验,就利用金刚石滚轮对砂轮进行修整,在每一组磨削实验前均要进行修锐,以保证砂轮状态一致性。在相同的工装条件下,磨削工艺参数的变化将直接影响工件表面质量,合理的工艺参数能够保证加工目标的实现,具体的磨削工况及表面粗糙度测量值见表1。
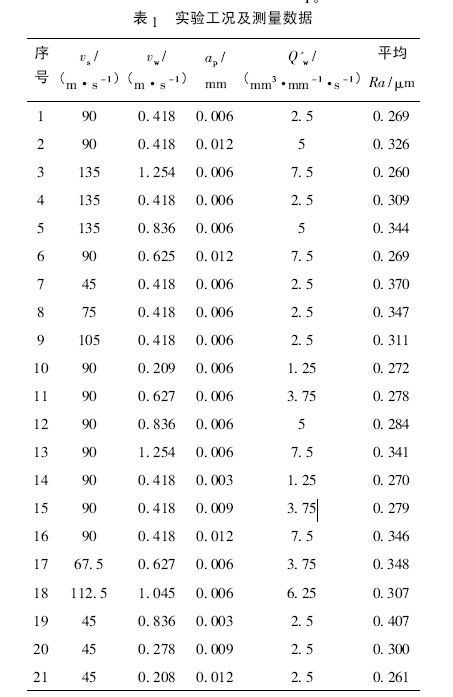
3. 3 数据的归一化处理
网络训练和执行时,必须对输入输出参数中的非数值数据进行量化、数值数据进行归一化处理,这样有利于RBF 神经网络在训练过程中收敛速度更快,效果更佳。
对实验数据( 砂轮线速度、工件速度、磨削深度、材料去除率、表面粗糙度) 进行归一化处理,将数据处理为区间[0,1] 之间的数据。归一化方法有很多形式,这里采用式( 3) 进行归一化处理。
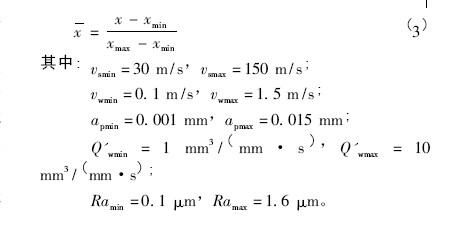
3. 4 RBF 网络的设计
3. 4. 1 输入输出参数的设定
在建立RBF 神经网络模型时,将影响工件表面粗糙度的主要因素作为网络输入层参数,输出层参数则为表面粗糙度。确定网络模型各层参数如下:输入样本为4 个磨削参数,输出样本为1 个,RBF网络的隐含层神经元则由训练过程决定。网络的目标误差设定为0. 000 1,神经元最大个数设定为50,两次显示之间所添加的神经元数目设定为1。故此神经网络结构的确定重点是隐层神经元个数的确定。
3. 4. 2 隐层神经元个数的确定
在RBF 神经网络模型的建立中,隐含层神经元的个数是影响网络预测性能的重要因素。确定的有效方法是在RBF 网络的训练过程中,通过选取不同宽度系数SPREAD 的值对网络进行训练,通过训练得到的各个网络的预报精度及训练次数,来确定网络最佳的隐含层神经元数。
通过循环算法设计了一个宽度系数值SPREAD可变的训练算法,通过误差对比,确定最佳的隐层神经元个数。其中的训练样本来源于表2 中1—16 组实验数据。不同SPREAD 值条件下的训练情况如表3 所示。

在SPREAD 值为2 时,虽然其训练次数多了1 次,但其所能达到的预报精度远远高于其他4 组值( 训练结果如图4 所示) 。因此该网络宽度系数值SPREAD 选为2,此时网络的训练次数为15 次,网络模型的隐层神经元个数为15 个,故RBF 网络结构可确定为4—15—1。

4 预测结果及分析
为了验证此神经网络模型的预测效果,抽取表2中17—21 组数据进行预测,其预测结果如表4 所示。
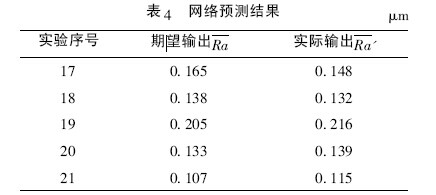
从表4 可以看出: 期望输出和实际输出的数值差值还是在可以接受的范围之内,预测准确率在85%以上。这说明此磨削表面粗糙度智能预测模型在实际工作中也可发挥作用,体现了其实用价值。
5 结论
(1) 通过MATLAB 实现了RBF 神经网络的表面粗糙度的预测模型,解决了传统方法对非线性预测精度不高和复杂建模的问题。
(2) 在RBF 神经网络模型的建立中,隐含层神经元的个数是影响网络预测性能的重要因素。采用循环算法,选取不同宽度系数SPREAD 的值对网络进行训练,通过训练得出各个网络的预报精度及训练次数,以此来确定网络最佳的隐含层神经元数。
(3) 从提高智能预测模型预测准确率的角度出发,还可以加入更多的样本数据用以反复的训练,这样训练出来的网络的精确度更高,模型预测出的结果更接近实际情况。
(4) 该预测模型的准确率可以达到85% 以上,相对误差远小于使用经验公式分析时的相对误差,对磨削表面粗糙度的预测研究具有一定的参考和应用价值。
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com










