伺服控制系统的复合模糊自适应 PID 控制
摘要: 以工程中的伺服控制系统为研究对象,提出一种嵌入比例因子的复合模糊自适应 PID 控制方法,即将比例因子模糊控制与模糊 PID 控制结合而成的复合模糊控制。首先通过 MATLAB /Simulink系统工具对无干扰理想状况下的系统进行仿真与分析,然后进一步模拟真实环境下的系统运行状况,在某一时刻加入干扰信号,并将比例因子模糊控制嵌入模糊 PID 控制中优化算法,对控制系统不断加以改善与优化。试验结果表明,此方法比传统 PID 控制更具优势,能有效改善控制系统的响应时间、调节时间以及抗干扰能力,有效提高控制系统的动态性能和鲁棒性。
关键词: 伺服控制系统; 传统 PID 控制; 模糊自适应 PID; 比例因子
0、 引言
当前智能控制算法的伺服控制系统应用较为广泛,对系统实时性、稳定性、抗干扰能力等方面要求较高。伺服控制系统具有非线性及未知性,系统运转过程中常会遇到未知的突发状况等干扰,需及时进行自我调节并能在有效范围内快速恢复平稳状态。陈智勇等采用电流、位置、速度三闭环的控制方式与电压矢量调制控制算法实现伺服控制; 武星等采用多目标遗传算法优化伺服控制器的 PID 参数方法实现伺服控制; S. Kissling采用迭代反馈整定的方式实现对伺服系统的控制参数进行整定。综合国内外相关伺服控制算法,各有利弊,应结合实验背景及应用领域对控制算法进行研究。文章提出一种嵌入比例因子的复合模糊自适应 PID 控制方法,在广泛应用的模糊 PID 控制算法中嵌入比例因子进行复合模糊控制。简单 PID 仅限于数学模型精确的控制系统,而模糊 PID 控制算法有适应非线性和时变性等优点,其抗干扰能力强、动态性能好,且无需精确数学模型。控制系统将模糊自适应 PID 控制与 PLC 结合,采用模糊自适应 PID 控制算法对参数自调整,通过 PLC 实现模糊自适应控制策略,可提升伺服控制系统的响应时间、控制精度和平稳性。
1 、伺服自适应控制系统模型
1. 1 模糊自适应
PID 控制算法传统 PID 算法单一,复杂工况下无法对参数进行实时自整定。尤其应用在特殊环境下的伺服控制系统,例如转运核废料的智能起重机,在扰动环境下,系统实时性与鲁棒性较差。对模糊自适应 PID 控制系统而言,需找出 PID 的系统参数 kp、ki、kd与偏差 e 、偏差变化率 ec 间的模糊关系,通过不断检测 e 和 ec 的方式,基于模糊控制原理对 3 个控制参数调整,使伺服系统具有良好的动静态性能,其系统结构见图 1。
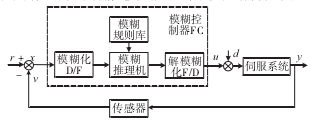
图 1 模糊自适应 PID 伺服控制系统框图
以误差 e 和误差变化率 ec 作为输入,模糊控制自整定参数 ΔKp、ΔKi及 ΔKd作为输出,将输入输出的模糊论域均设定为{ - 3,- 2,- 1,0,1,2,3} ,则对应的模糊子集为{ NB,NM,NS,Z,PS,PM,PB} ,并且采用对称分布的三角形隶属函数。模糊控制规则是模糊控制器设计的核心,模糊控制规则采用如下格式:if E is A and EC is B,then U is CPID 参数自调整规则可总结为表 1 ~ 表 3。

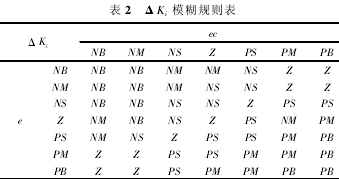


1. 2 系统模型设计
以伺服控制系统为对象,采用模糊自适应 PID 控制算法,通过 PLC 实现对伺服电机的控制。伺服电机分为转矩控制、位置控制和速度控制等模式,考虑各方式特性,结合系统的功能需求,选取合适的控制模式。基于位置控制模式,通过 PLC 输出对应的脉冲信号到伺服驱动器,需设置相应的增益参数对数据进行关系转换。基于图 1 伺服控制系统框图,建立如图 2 所示的系统仿真模型,并将传统 PID 控制与模糊自适应 PID 控制并行试验,分别对系统的响应特性、超调量、调节时间、平稳性等方面进行比较分析。比例系数可加快系统的响应速度,减小系统稳态误差; 积分系数可消除系统的稳态误差,但太大会在响应过程的初期产生积分饱和; 微分系数可改善系统的动态特性,若过大则会延长调节时间,从而降低系统的抗干扰性。总结对应的特性与优劣,并依据试验结果,结合工程中实际运用条件,对系统不断进行优化改善,使此控制系统达到较为良好的控制效果。
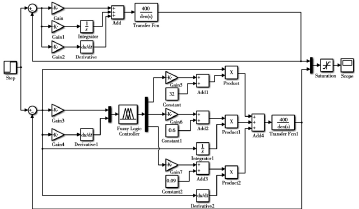
图 2 系统初步仿真模型图
建立系统模型,并对其进行仿真实验,仿真过程中需要对各环节的增益、常数修正值等系统参数进行对应调整,其中 PID 的主要参数 kp、ki和 kd对系统平稳性、稳态精度和超调量等控制性能指标均有重要影响。从系统的动静态综合性能角度考虑,在不同的误差 e和误差变化率 ec 状况下,控制过程对参数自整定也会有不同的要求,常常参考实际工程经验总结出的参数自整定原则,并结合误差 e 和误差变化率 ec ,可根据系统的响应速度、震荡程度、趋于稳定的时间长短等等实际运行状况,进行参数自整定调整。参数自整定的取值较大较小是针对对应参数初始值而言,在实际应用中 PID 参数是基于其初值而自调整得出,即:

1. 3 系统模型优化
根据建立的系统仿真模型试验,经过不断的调试使控制系统的响应速度、超调量、稳定性等指标逐渐达标,可达到较好的控制效果。但是在实际工程运用中,系统时常会出现不定时干扰或负载发生变化等未知状况,因此需要对系统进一步优化与改善。广泛应用于工业领域的伺服控制系统应具有高精度与良好的实时性,则需要将控制率的计算量尽可能减小,并在一定条件下,对外界未知扰动应满足较好的鲁棒性。因此,通过嵌入比例因子的模糊控制,在线修正比例、微分环节,对系统进一步进行优化。在未知扰动、负载发生变化或启动误差较大时,会使误差 e 发生一定的跳变,嵌入比例因子的模糊控制环节进行自我调节,使系统快速响应并跟踪其参考信号,从而改善系统的鲁棒性与动态性能。在运行各阶段,系统对比例因子的需求并不相同,根据系统的运行状况对控制量在线整定,可大大改善系统的控制效果,比例因子a、b 的模糊控制规则见表 4。

2 、仿真与分析

模拟仿真时,控制系统在无扰动环境下,选取仿真时长 t = 100s ,对控制系统以传统 PID 控制与模糊自适应 PID 控制两种控制方式进行并行试验,分别对其进行比较、分析以及调试,使运行结果达到较为满意的效果,系统运行曲线如图 3 所示,其局部放大示意图见图 4.
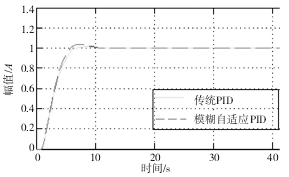
图 3 理想型系统运行曲线图.
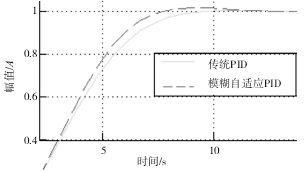
图 4 理想型系统运行曲线局部放大示意图
从上图系统运行曲线可知,两种 PID 控制方式下系统性能都较好,二者均能快速趋于平稳,减少对应的调节时间。虽然传统 PID 控制比模糊自适应 PID 控制平稳且没有超调量,但是模糊自适应 PID 控制在具有更快的响应速度下也能快速趋于平稳,若在系统运行可靠环境下更能提高系统工作效率。
2. 2 优化型复合模糊自适应
PID 控制在实际环境下,难以避免出现负载变化等扰动现象。因此,模拟真实环境下,考虑干扰因素,在某一时刻对系统加入干扰信号,并对模糊自适应 PID 控制与比例因子结合进行复合模糊控制。
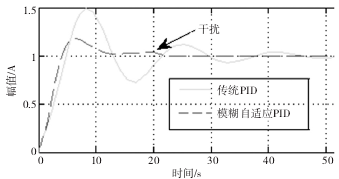
图 5 优化型系统运行曲线图
选取仿真时间 t = 100 s,对系统分别采用传统PID 控制与模糊自适应 PID 复合控制进行试验,系统运行曲线图如图 5 所示。根据图 5 系统运行曲线,传统 PID 控制下系统的响应速度较慢,会产生较大超调量,在一段时间内震荡剧烈,系统反应速度较慢,且调节时间更久,系统的鲁棒性较差。在 t = 20 s 时加入扰动,虽在短时间内模糊自适应控制下系统也会产生较小的超调量,但系统响应较快,能快速检测到干扰并能及时进行自我调整,几乎能在 2s 内快速趋于平稳,且没有过于明显的震荡,能有效提高系统的动态性能,使系统的控制效果更佳,其局部示意图见图 6、图 7。
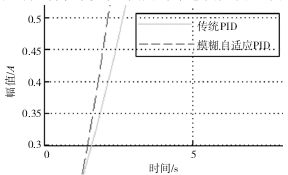
图 6 快速响应局部示意图
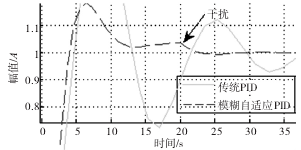
图 7 抗干扰局部示意图
3 、总结
模糊自适应 PID 复合控制方法对于受控系统一方面无需具备准确的数学模型,另一方面也可对参数进行自调整。文章在 MATLAB/Simulink 系统工具下,基于模糊 PID控制算法,并且分别在传统 PID 控制、模糊 PID 控制以及改进后的复合模糊自适应控制环境下,对自适应伺服系统进行模拟试验、分析与优化。试验结果表明,模糊自适应PID 控制算法具有良好的控制效果,能有效改善系统的响应速度,缩短调节时间以及增强系统的抗干扰能力,可有效改善系统的动态性能和鲁棒性。此外,在工程应用中亦可提高自适应控制系统的可行性,使控制系统更具智能化,具有重要的应用价值。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息
- target=_blank>适用于网络化农业机械制造模式的数控系统的研究
- target=_blank>美国 HAAS 机床国产化数控系统的改造
- target=_blank>基于 PLC 和触摸屏的数控钻床控制系统
- target=_blank>数控轧辊磨床磨削技术的新方向——4点测量3D磨削
- target=_blank>创新机器人热成形件激光切割解决方案









