基于普通数控车床的等距型面加工研究
2021-5-6 来源:沈阳理工大学机械 内蒙古北方重工业 作者:姜增辉 姜智勇 张宇庭 仉智宝 马立久
摘 要: 等距型面连接在重载机械的大扭矩传递中已呈现取代传统键连接的趋势。目前常采用加工中心来完成等距型面的切削加工。提出了一种应用普通两轴数控车床加工等距型面的方法,利用 G32 指令车削端面螺纹的功能代替加工中心的 C 轴功能,实现切削中圆周角度的精确定位与跟踪。建立了利用 G32 指令拟合加工等距型面的模型,并设计了相应宏程序。建立了基于 VERICUT 的仿真切削环境,并进行了车削仿真加工。结果表明,应用普通两轴数控车床可以实现等距型面的切削加工,且选取适合的分割增量角对保证加工精度非常重要。
关键词: 等距型面; 数控车床; 车削; 宏程序; 仿真加工
型面连接相比键连接具有更好的对中性,更小的应力集中和更大的连接刚度,其在大扭矩传递中逐渐得到了广泛应用。在型面连接中,其廓形曲线以等距廓形曲线应用最为广泛。等距型面连接加工可以采用靠模仿型法和机械式运动合成法实现,但这些方法制造柔性差,生产效率低。目前,通常在三轴以上加工中心上采用车削或铣削方式完成等距型面的加工,这大大提高了加工设备成本在零件制造成本中的占比,也使得一些加工中心较少的小微加工企业不得不放弃这类产品的生产订单。
为解决这一问题,提出了一种在普通两轴数控车床上,利用 G32 指令加工等距型面的方法。
1 、基于 G32 的等距型面车削原理
等距型面是一种非回转体型面,普通两轴数控车床在利用直线插补指令 G01 车削加工中不能实现车刀在工件圆周方向的定位和跟踪,因此无法通过 G01利用 X、Z 轴联动完成等距型面加工。螺纹车削指令 G32 可以通过调用主轴编码器实现主轴转速和车刀进给之间的精确配合,由此可以利用 G32 以阿基米德螺旋线拟合等距型面曲线,在普通两轴数控车床上实现等距型面的加工。
1.1 G32 车削等距型面原理
G32 为单行程车削螺纹指令,加工端面螺纹时,X轴进给和主轴转动进行闭环联动,由此可以将等距型面廓形曲线拆分成小段曲线,用 G32 逐段拟合。为进行拟合加工对等距廓形曲线进行等弧长分割,可得到分割点 P1、P2,…,Pi,…,Pn。用 G32 指令以上述分割点依次为起、终点逐段拟合等距廓形曲线,可实现等距型面的加工。G32 指令的代码一般结构为:G32 X( U) Z( W) F( I) Q其中: X 为终止点的极径; Z 为终止点 Z 轴坐标; F 为螺纹螺距,即主轴旋转一圈 X 方向的增量; Q 为起始点角度。
若应用 G32 代码拟合加工等距型面,需确定加工每一段被分割的等 弧长 曲 线 时 参 量 X、Z、F、Q 的赋值。以如图 1 所示等距三边型面为例,其等距廓形曲线由小圆弧 AB 和大圆弧 BC 构成的廓形曲线段 AC 以120°中心对称所得,因此实现 AC 段曲线的拟合加工,即可实现完整等距三边廓形的加工。选小弧中点 P0( 即 D 点) 为起刀点,此处进、退刀不易划伤已加工表面。由于圆弧 AD 与 CE 以 O 点呈 120°的中心对称,则前述对 AC 段曲线的加工转化为了对 DE 段曲线的加工。下面就如何求得拟合加工曲线段 DE 时 G32 代码的各参量赋值进行分析。
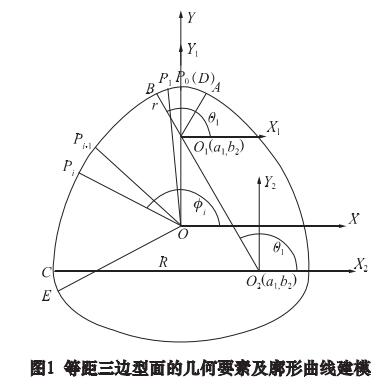
1.2 X 的赋值分析

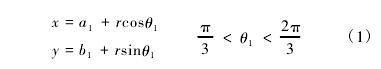
由于小圆弧 AD 与 CE 以 O 点呈 120°的中心对称,式( 1) 对于小圆弧 CE 在以其自身圆心为原点建立的小圆弧相对坐标系内同样成立。大圆弧 BC 在绝对坐标系 XOY 内的方程为:

1.3 Z、F 的赋值分析
与 X 的的赋值类似,在对每一段被分割曲线弧的拟合加工时参量 Z 也需重新赋值。

1.4 廓形曲线的分割及 Q 的赋值分析
如图 1 所示,拟合加工曲线 DE 的起刀点 P0( D)在小圆弧 AB 上,由此先对小圆弧 AB 进行分割,且其中对小圆弧 AD 部分的分割,其方法对小圆弧 CE 同样成立。

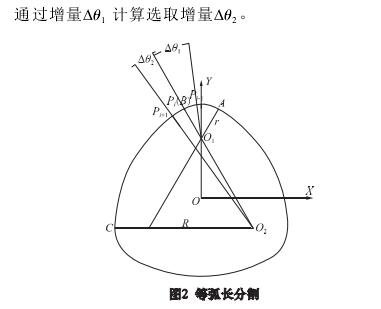


2 、宏程序设计
在拟合车削等距三边型面的数控程序中,指令G32 中 4 个参量的赋值计算是核心内容。为此,设计参量赋值宏程序如图 3 所示。
通过宏程序实现等弧长分割,完成分割点坐标、极径和极角的计算,并对 G32 代码中的参量进行赋值。
3 、等距三边型面的虚拟加工
通过虚拟加工等距三边型面验证以 G32 拟合车削等距型面的可行性。毛坯选择直径 101 mm 长 400mm 的中碳钢棒料,拟加工得到大径 50 mm 小径 41.38mm 的等距三边型面。
3.1 加工参数
为提高切削效率,保证加工质量,采用切削深度、轴向进给量逐渐递减,低速粗车、高速精车的切削参数选择方案。拟进行四刀粗车、一刀精车,其加工刀路如图 4 所示,切削参数如表 1 所示。车削参数粗车最后一刀留有偏置余量 0.31 mm,这样精车背吃刀量恒定,提高加工精度。
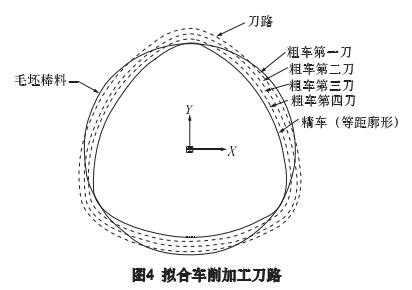
表 1 车削加工切削参数
3.2 构建虚拟机床
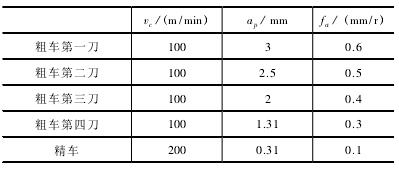
根据被加工件尺寸选用 MJ-460 数控车床为原型建立虚拟机床。该机床只具备 X、Z 轴,没有 C 轴功能,其斜床身利于排屑,有更好的稳定性。
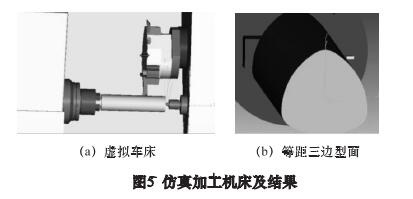
通过 UG 建立机床部件的 STL 模型文件,并导入VERICUT 中构建虚拟车床 ( 如图 5a) ,并由表 1 切削参数仿真加工得到等距三边型面( 如图 5b) 。
4 、仿真结果与分析
如前所述可知,等距曲线的分割增量角,即小圆弧圆心角增量!θ1,对加工精度有很大影响。为研究!θ1对加工精度的影响规律,分别取!θ1为 1°、2°、3°和 4°进行了仿真切削,并采用 VERICUT 距离测量工具对加工误差进行了测量。测量位置如图 6 所示位置,包括等距廓形曲线在小弧顶点、大弧顶点及大弧与小弧相切点共 12 个特征点。结果如图 7 所示。
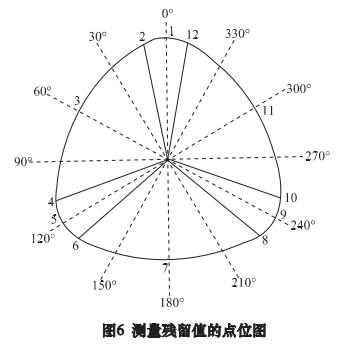
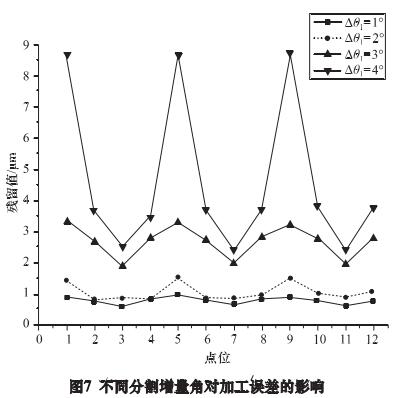
由图 7 可知,所测点位加工误差均为残留,无过切发生。测量点位中小弧顶点残留值最大,大弧顶点残留值最小,这是由于拟合加工等距廓形时,采用了等弧长方法对廓形曲线进行分割,而小弧段分割曲线段曲率相对较大,导致拟合间隙也较大,因此加工残留相应较大。
另外,加工误差与分割增量角并非线性增加关系,增量角增大可导致最大误差的增幅迅速变大,且加工误差在等距廓形上的波动幅度也迅速变大。因此,选取较小的分割增量角有利于提高廓形的加工精度。但应注意,实际加工中受机床进给精度和数控系统预读速度的影响,分割增量角不宜选取过小。
过小的增量角可使拟合加工中单步径向进给量小于机床径向进给精度,径向进给运动失真。另外,增量角越小,程序段越多,将导致数控系统的响应无法跟上加工路径执行速度,机床进给运动会减速、爬行,加工表面会因为程序的停顿而产生明显的刀痕。
5 、结语
建立了基于普通两轴数控车床 G32 指令的等距型面加工方法,设计了参量赋值宏程序,并通过构建虚拟机床进行了加工仿真,得到如下结果:
( 1) 通过 G32 指令可在普通两轴数控车床上实现等距型面的加工。
( 2) 选取合适的分割增量角对保证等距型面的表面加工精度十分重要。
减小分割增量角可降低已加工表面残留误差,并收窄误差波动幅度,但过小的分割增量角可能导致车削进给运动的减速和失真,反而降低已加工表面质量和精度。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





